Question

一架2.5m长的梯子斜靠在一竖直的墙上，这时梯脚距离墙角0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯脚移动的距离是（　　）

• A、0.4m
• B、0.9m
• C、0.8m
• D、1.8m

Answer 1

分析：梯子和墙面、地面形成的直角三角形，如下图所示可将该直角三角形等价于△ABC和△EFC，前者为原来的形状，后者则是下滑后的形状．由题意可得出AB=EF=2.5m，CB=0.7m，AE=0.4m，在Rt△ACB中，由勾股定理可得：AB²=AC²+BC²，将AB、CB的值代入该式求出AC的值，EC=AC-AE；在Rt△ECF中，由勾股定理可得：EF²=EC²+CF²，即：CF²=EF²-（AC-AE）²，求出CF的值，BF=CF=CB，即求出了梯脚移动的距离．

解答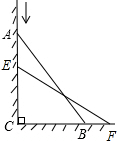：解：如下图所示：AB相当于梯子，△ABC是梯子和墙面、地面形成的直角三角形，△EFC是下滑后的形状，∠C=90°，
即：AB=EF=2.5m，CB=0.7m，AE=0.4m，BF是梯脚移动的距离．
在Rt△ACB中，由勾股定理可得：
AB²=AC²+BC²，
AC=

AB2-BC2

=

(2.5)2-(0.7)2

=2.4m．
∴EC=AC-AE=2.4-0.4=2m，
在Rt△ECF中，由勾股定理可得：
EF²=EC²+CF²，
CF=

EF2-EC2

=

(2.5)2-22

=1.5m，
BF=CF-CB=1.5-0.7=0.8m，
即：梯脚移动的距离为0.8m．
故选C．

点评：本题主要考查勾股定理在实际中的应用，通过作相应的等价图形，可以使解答更加清晰明了．