题目内容
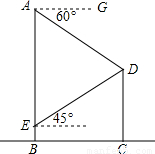
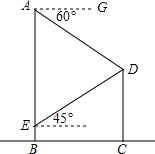 如图,已知楼AB的高为30米,从楼顶A处测得旗杆CD的顶端D的俯角为60°,又从楼AB离地面5米处的窗口E测得旗杆的顶端C仰角为45°,求:旗杆CD的长.(精确到0.1m)
如图,已知楼AB的高为30米,从楼顶A处测得旗杆CD的顶端D的俯角为60°,又从楼AB离地面5米处的窗口E测得旗杆的顶端C仰角为45°,求:旗杆CD的长.(精确到0.1m)
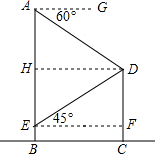 解:如图:过点E作EF⊥CD于F,过点D作DH⊥AB于H,
解:如图:过点E作EF⊥CD于F,过点D作DH⊥AB于H,∴DH∥EF∥BC,
∴∠ADH=∠GAD=60°,
∴四边形EFDH与四边形BCFE是矩形,
∴DF=EH,CF=BE=5,DH=EF,
设DF=xm,
∴EH=DF=xm,
在Rt△DEF中,∠DFE=90°,∠DEF=45°,
∴DH=EF=
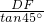 =DF=x(m),
=DF=x(m),在Rt△ADH中,AH=DH•tan60°=
 x(m),
x(m),∵AB=30m,
∴
 x+x+5=30,
x+x+5=30,解得:x=
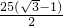 ≈9.2(m),
≈9.2(m),即DF=9.2m,
∴CD=DF+CF=9.2+5=14.2(m).
∴旗杆CD的长为14.2m.
分析:首先过点E作EF⊥CD于F,过点D作DH⊥AB于H,易得四边形EFDH与四边形BCFE是矩形,设DF=xm,在Rt△ADH中与Rt△DEF中,利用正切函数,即可表示出AH,EH的长,又由楼AB的高为30米,即可得方程,解此方程即可求得答案.
点评:本题考查仰角与俯角的定义.此题难度适中,注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
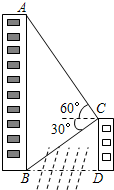 如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°.求两座楼房的底部BD之间的距离.
如图,某条河的两岸建有两座楼房.已知写字楼AB的高为80米,小明站在河对岸的一座办公楼CD的楼顶C点处,测得写字楼的楼顶A点处的仰角为60°,测得楼底B点处的俯角为30°.求两座楼房的底部BD之间的距离.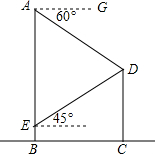 (2006•河北区一模)如图,已知楼AB的高为30米,从楼顶A处测得旗杆CD的顶端D的俯角为60°,又从楼AB离地面5米处的窗口E测得旗杆的顶端C仰角为45°,求:旗杆CD的长.(精确到0.1m)
(2006•河北区一模)如图,已知楼AB的高为30米,从楼顶A处测得旗杆CD的顶端D的俯角为60°,又从楼AB离地面5米处的窗口E测得旗杆的顶端C仰角为45°,求:旗杆CD的长.(精确到0.1m) 如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.
如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.