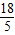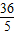题目内容
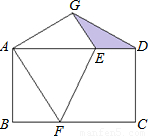
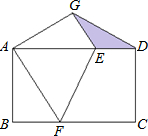如图所示，在完全重合放置的两张矩形纸片ABCD中，AB=4，BC=8，将上面的矩形纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为G，连接DG，则图中阴影部分的面积为| 18 |
| 5 |
| 18 |
| 5 |
分析：由于AF=CF，则在Rt△ABF中由勾股定理求得AF的值，证得△ABF≌△AGE，有AE=AF，即ED=AD-AE，再由直角三角形的面积公式求得Rt△AGE中边AE上的高的值，即可计算阴影部分的面积．
解答：解：由题意知，AF=FC，AB=CD=AG=4，BC=AD=8
在Rt△ABF中，由勾股定理知AB2+BF2=AF2，即42+（8-AF）2=AF2，
解得：AF=5，
∵∠BAF+∠FAE=∠FAE+∠EAG=90°，
∴∠BAF=∠EAG，
∵∠B=∠AGE=90°，AB=AG，
∴△BAF≌△GAE，
∴AE=AF=5，ED=GE=3
∵S△GAE=
AG•GE=
AE•AE边上的高
∴AE边上的高=
，
∴S△GED=
ED•AE边上的高=
×3×
=
．
故答案为：
．
在Rt△ABF中，由勾股定理知AB2+BF2=AF2，即42+（8-AF）2=AF2，
解得：AF=5，
∵∠BAF+∠FAE=∠FAE+∠EAG=90°，
∴∠BAF=∠EAG，
∵∠B=∠AGE=90°，AB=AG，
∴△BAF≌△GAE，
∴AE=AF=5，ED=GE=3
∵S△GAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE边上的高=
| 12 |
| 5 |
∴S△GED=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
| 18 |
| 5 |
故答案为：
| 18 |
| 5 |
点评：本题利用了矩形的性质和翻折的性质、勾股定理、全等三角形的判定和性质求解，注意翻折前后对应边相等，难度一般．
练习册系列答案
天天向上口算本系列答案
相关题目
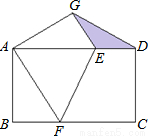
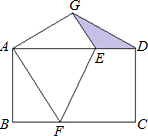如图所示，在完全重合放置的两张矩形纸片ABCD中，AB=4，BC=8，将上面的矩形纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为G，连接DG，则图中阴影部分的面积为（ ）A、
| ||||
| B、6 | ||||
C、
| ||||
D、
|
