题目内容
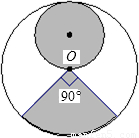
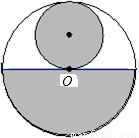
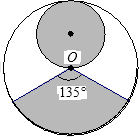
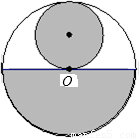
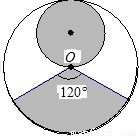
从一张半径为R圆形纸板剪出一个圆形和一个扇形,分别作为圆锥体的底面和侧面,下列的剪法(小圆的半径都为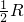 )恰好配成一个圆锥体的是
)恰好配成一个圆锥体的是
- A.

- B.

- C.

- D.
B
分析:根据圆锥的底面圆的周长等于扇形弧长,只要图形中两者相等即可配成一个圆锥体,求出圆心角即可.
解答:根据圆锥的底面圆的周长等于扇形弧长,只要图形中两者相等即可配成一个圆锥体,
∵小圆的半径都为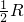 ,
,
∴圆锥的底面圆的周长等于2π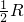 =πR,
=πR,
扇形弧长为: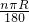 =πR,
=πR,
∴n=180°,
∴扇形圆心角等于180°,
故选:B.
点评:此题主要考查了圆锥的计算,得出圆锥的底面圆的周长等于扇形弧长是解决问题的关键.
分析:根据圆锥的底面圆的周长等于扇形弧长,只要图形中两者相等即可配成一个圆锥体,求出圆心角即可.
解答:根据圆锥的底面圆的周长等于扇形弧长,只要图形中两者相等即可配成一个圆锥体,
∵小圆的半径都为
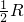 ,
,∴圆锥的底面圆的周长等于2π
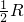 =πR,
=πR,扇形弧长为:
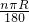 =πR,
=πR,∴n=180°,
∴扇形圆心角等于180°,
故选:B.
点评:此题主要考查了圆锥的计算,得出圆锥的底面圆的周长等于扇形弧长是解决问题的关键.

练习册系列答案
相关题目
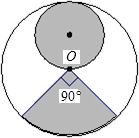
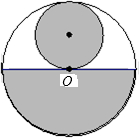
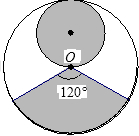
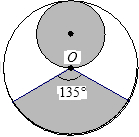
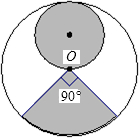
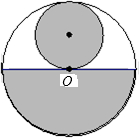
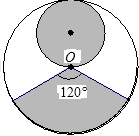
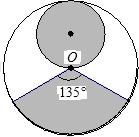
 )恰好配成一个圆锥体的是( )
)恰好配成一个圆锥体的是( )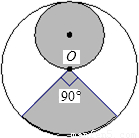



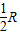 )恰好配成一个圆锥体的是( )
)恰好配成一个圆锥体的是( )

 )恰好配成一个圆锥体的是( )
)恰好配成一个圆锥体的是( )