题目内容
如图所示,点B坐标为(18,0),点A坐标为(18,6),动点P从点O开始沿OB以每秒3个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒1个单位长度的速度向点A移动.如果P、Q分别从O、B同时出发,用t(秒)表示移动的时间(0<t≤6),那么,(1)当t=______时,以点P、B、Q为顶点的三角形与△AOB相似;
(2)若设四边形OPQA的面积为y,试写出y与t的函数关系式,并求出t取何值时,四边形OPQA的面积最小?
(3)在y轴上是否存在点E,使点P、Q在移动过程中,以B、Q、E、P为顶点的四边形的面积是一个常数,请求出点E的坐标;若不存在,请说明理由.

【答案】分析:(1)讨论:当∠BPQ=∠BOA,即PQ∥OA,由相似三角形:Rt△QPB∽Rt△AOB,的对应边成比例求得t=3;当∠BPQ=∠A,则Rt△BPQ∽Rt△BAO,由相似三角形的对应边成比例知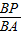 =
=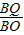 ,即
,即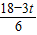 =
=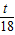 ,即可得到t=5.4;
,即可得到t=5.4;
(2)利用y=S△OAB-S△BPQ= ×18×6-
×18×6- ×(18-3t)t,然后利用配方法求得该二次函数的最值,即求出t取何值时,四边形OPQA的面积最小;
×(18-3t)t,然后利用配方法求得该二次函数的最值,即求出t取何值时,四边形OPQA的面积最小;
(3)当点E在y轴正半轴时,利用以B、Q、E、P为顶点的四边形的面积=梯形BQEO的面积-△OPE的面积,用t与m表示出来为 (t+m)×18-
(t+m)×18- ×3t×m=(9-
×3t×m=(9- m)t+9m,当t的系数为0时即可得到m的值;
m)t+9m,当t的系数为0时即可得到m的值;
当点E在y轴负半轴时,S=S△EPB+S△PBQ= (18-3t)(-m)-
(18-3t)(-m)- (18-3t)t=-
(18-3t)t=- t2+
t2+ mt+9t-9m.此时不存在m的值,使S的值为常数.
mt+9t-9m.此时不存在m的值,使S的值为常数.
解答: 解:∵点B坐标为(18,0),点A坐标为(18,6),
解:∵点B坐标为(18,0),点A坐标为(18,6),
∴BO=18,AB=6,AB⊥0B.
(1)当∠BPQ=∠BOA,即PQ∥OA,Rt△QPB∽Rt△AOB,
则 =
= ,即
,即 =
= ,
,
解得t=3;
当∠BPQ=∠A,则Rt△BPQ∽Rt△BAO,
∴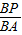 =
= ,即
,即 =
= ,
,
∴t=5.4.
所以当t=3秒或5.4秒时,以点P、Q、B为顶点的三角形与△AOB相似.
(2)y=S△OAB-S△BPQ= ×18×6-
×18×6- ×(18-3t)t=
×(18-3t)t= (t-3)2+
(t-3)2+ ,即y=
,即y= (t-3)2+
(t-3)2+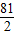 .
.
则当t=3,四边形OPQA的面积最小;
(3)存在.理由如下:
设以B、Q、E、P为顶点的四边形面积是S,E(0,m).
①如图1,当E在y轴的正半轴上时,则
S=S梯形BQEO-S△OPE= (t+m)×18-
(t+m)×18- ×3t×m=(9-
×3t×m=(9- m)t+9m.
m)t+9m.
故当9- m=0,即m=6时,S=54是一个定值;
m=0,即m=6时,S=54是一个定值;
②如图2,当点E在y轴的正半轴上时,则S=S△EPB+S△PBQ= (18-3t)(-m)-
(18-3t)(-m)- (18-3t)t=-
(18-3t)t=- t2+
t2+ mt+9t-9m.
mt+9t-9m.
此时不存在m的值,使S的值为常数.
综上所述,点E的坐标(0,6)使点P、Q在移动过程中,以B、Q、E、P为顶点的四边形的面积是一个常数.
故答案为:3或5.4.
点评:本题考查了三角形相似的判定与性质:两组对应角相等的三角形相似;相似三角形的对应边的比相等.也考查了分类讨论思想的运用以及三角形的面积公式.
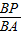 =
=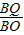 ,即
,即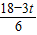 =
=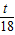 ,即可得到t=5.4;
,即可得到t=5.4;(2)利用y=S△OAB-S△BPQ=
 ×18×6-
×18×6- ×(18-3t)t,然后利用配方法求得该二次函数的最值,即求出t取何值时,四边形OPQA的面积最小;
×(18-3t)t,然后利用配方法求得该二次函数的最值,即求出t取何值时,四边形OPQA的面积最小;(3)当点E在y轴正半轴时,利用以B、Q、E、P为顶点的四边形的面积=梯形BQEO的面积-△OPE的面积,用t与m表示出来为
 (t+m)×18-
(t+m)×18- ×3t×m=(9-
×3t×m=(9- m)t+9m,当t的系数为0时即可得到m的值;
m)t+9m,当t的系数为0时即可得到m的值;当点E在y轴负半轴时,S=S△EPB+S△PBQ=
 (18-3t)(-m)-
(18-3t)(-m)- (18-3t)t=-
(18-3t)t=- t2+
t2+ mt+9t-9m.此时不存在m的值,使S的值为常数.
mt+9t-9m.此时不存在m的值,使S的值为常数.解答:
 解:∵点B坐标为(18,0),点A坐标为(18,6),
解:∵点B坐标为(18,0),点A坐标为(18,6),∴BO=18,AB=6,AB⊥0B.
(1)当∠BPQ=∠BOA,即PQ∥OA,Rt△QPB∽Rt△AOB,
则
 =
= ,即
,即 =
= ,
,解得t=3;
当∠BPQ=∠A,则Rt△BPQ∽Rt△BAO,
∴
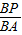 =
= ,即
,即 =
= ,
,∴t=5.4.
所以当t=3秒或5.4秒时,以点P、Q、B为顶点的三角形与△AOB相似.
(2)y=S△OAB-S△BPQ=
 ×18×6-
×18×6- ×(18-3t)t=
×(18-3t)t= (t-3)2+
(t-3)2+ ,即y=
,即y= (t-3)2+
(t-3)2+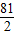 .
.则当t=3,四边形OPQA的面积最小;
(3)存在.理由如下:
设以B、Q、E、P为顶点的四边形面积是S,E(0,m).
①如图1,当E在y轴的正半轴上时,则
S=S梯形BQEO-S△OPE=
 (t+m)×18-
(t+m)×18- ×3t×m=(9-
×3t×m=(9- m)t+9m.
m)t+9m.故当9-
 m=0,即m=6时,S=54是一个定值;
m=0,即m=6时,S=54是一个定值;②如图2,当点E在y轴的正半轴上时,则S=S△EPB+S△PBQ=
 (18-3t)(-m)-
(18-3t)(-m)- (18-3t)t=-
(18-3t)t=- t2+
t2+ mt+9t-9m.
mt+9t-9m.此时不存在m的值,使S的值为常数.
综上所述,点E的坐标(0,6)使点P、Q在移动过程中,以B、Q、E、P为顶点的四边形的面积是一个常数.
故答案为:3或5.4.
点评:本题考查了三角形相似的判定与性质:两组对应角相等的三角形相似;相似三角形的对应边的比相等.也考查了分类讨论思想的运用以及三角形的面积公式.

练习册系列答案
相关题目
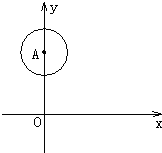 26、如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上.
26、如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上. (0<t≤6),那么,
(0<t≤6),那么,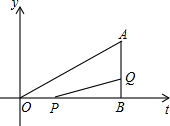 (2013•吴江市模拟)如图所示,点B坐标为(18,0),点A坐标为(18,6),动点P从点O开始沿OB以每秒3个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒1个单位长度的速度向点A移动.如果P、Q分别从O、B同时出发,用t(秒)表示移动的时间(0<t≤6),那么,
(2013•吴江市模拟)如图所示,点B坐标为(18,0),点A坐标为(18,6),动点P从点O开始沿OB以每秒3个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒1个单位长度的速度向点A移动.如果P、Q分别从O、B同时出发,用t(秒)表示移动的时间(0<t≤6),那么,