题目内容
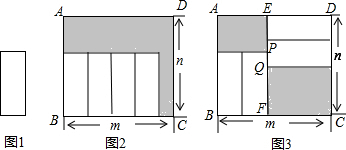
把四张形状大小完全相同的小长方形卡片（如图1）不重复地放在一个底面为长方形（长为m cm，宽为n cm）的盒子底部（如图2），盒子底面未被卡片覆盖的部分用阴影表示．则图2中两块阴影部分周长和是4n
4n
cm．（用m或n的式子表示）．分析：设小长方形卡片的长为xcm，宽为ycm，由图形得到m-x=2y，即x+2y=m，分别表示阴影部分两长方形的长与宽，进而表示出阴影部分的周长和，去括号合并后，将x+2y=m代入，即可得到结果．
解答：解：设小长方形卡片的长为xcm，宽为ycm，可得：m-x=2y，即x+2y=m，
根据近题意得：阴影部分的周长为2[（m-x）+（n-x）]+2[（n-2y）+（m-2y）]
=2（2m+2n-2x-4y）=4[m+n-（x+2y）]=4（m+n-m）=4n（cm）．
故答案为：4n
根据近题意得：阴影部分的周长为2[（m-x）+（n-x）]+2[（n-2y）+（m-2y）]
=2（2m+2n-2x-4y）=4[m+n-（x+2y）]=4（m+n-m）=4n（cm）．
故答案为：4n
点评：此题考查了整式加减运算的应用，弄清题意是解本题的关键．
练习册系列答案
相关题目
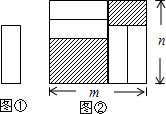
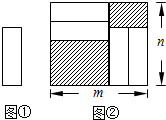
12、把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m cm，宽为n cm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分的周长和是（ ）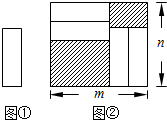
把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m cm，宽为n cm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分周长和是（ ）
