题目内容
已知甲、乙两人分别从相距18千米的A、B两地同时同向而行,甲以4千米/时的平均速度步行,乙以每小时比甲快1千米的平均速度步行,相遇为止.(1)求甲、乙两人相距的距离y(千米)和所用时间x(小时)的函数关系式;(2)求出函数图像与x轴、y轴的交点坐标,画出函数图像,并求出自变量的取值范围;(3)求当甲、乙两人相距6千米时,所需用的时间.
答案:
解析:
提示:
解析:
|
(1)y=-9x+18; (2)(2,0)(0,18),0≤x≤2; (3) |
提示:
|
(1)所设用时间为x,则甲走的路程为4x,乙走的路程为(4+1)x=5x,则两人相距的距离y=18-4x-5x=18-9x,即y=-9x+18.(2)当x=0时y=18;当y=0时x=2,则与x轴的交点为(2,0),与y轴的交点坐标(0,18).(3)当两人相距6千米时,则6=18-9x,解得x=
|

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

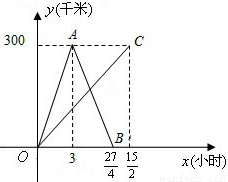
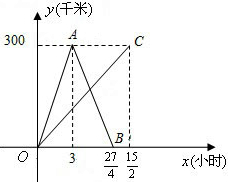 地,乙从B地直接到达A地,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
地,乙从B地直接到达A地,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.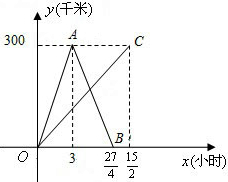 地,乙从B地直接到达A地,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
地,乙从B地直接到达A地,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.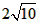 千米?
千米?