题目内容
已知⊙O的直径为15,弦AB∥CD,AB=9,CD=12,那么两弦的距离是 .
考点:垂径定理,勾股定理
专题:计算题,分类讨论
分析:分两种情况考虑:当两条弦位于圆心O一侧时,如图1所示,过O作OE⊥AB于点E,交CD于点F,连接OA,OC,交AB于点F,连接OA,OC,由AB∥CD,得到OE⊥AB,利用垂径定理得到E与F分别为CD与AB的中点,在直角三角形AOF中,利用勾股定理求出OF的长,在三角形COE中,利用勾股定理求出OE的长,由OE-OF即可求出EF的长;当两条弦位于圆心O两侧时,如图2所示,同理由OE+OF求出EF的长即可.
解答: 解:分两种情况考虑:
解:分两种情况考虑:
当两条弦位于圆心O一侧时,如图1所示,
过O作OE⊥AB,交CD于点F,交AB于点E,连接OA,OC,
∵AB∥CD,
∴OE⊥AB,
∴E、F分别为CD、AB的中点,
∴CF=DF=
CD=6cm,AE=BE=
AB=4.5cm,
在Rt△AOE中,OA=7.5cm,AE=4.5cm,
根据勾股定理得:OE=
=6cm,
在Rt△COF中,OC=7.5cm,CF=6cm,
根据勾股定理得:OF=
=
cm,
则EF=OE-OF=6-
=
cm;
当两条弦位于圆心O两侧时,如图2所示,同理可得EF=6+
=
cm,
综上,弦AB与CD的距离为
cm或
cm.
故答案为:
cm或
cm.
 解:分两种情况考虑:
解:分两种情况考虑:当两条弦位于圆心O一侧时,如图1所示,
过O作OE⊥AB,交CD于点F,交AB于点E,连接OA,OC,
∵AB∥CD,
∴OE⊥AB,
∴E、F分别为CD、AB的中点,
∴CF=DF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOE中,OA=7.5cm,AE=4.5cm,
根据勾股定理得:OE=
| 7.52-4.52 |
在Rt△COF中,OC=7.5cm,CF=6cm,
根据勾股定理得:OF=
| 7.52-62 |
| 9 |
| 2 |
则EF=OE-OF=6-
| 9 |
| 2 |
| 3 |
| 2 |
当两条弦位于圆心O两侧时,如图2所示,同理可得EF=6+
| 9 |
| 2 |
| 21 |
| 2 |
综上,弦AB与CD的距离为
| 3 |
| 2 |
| 21 |
| 2 |
故答案为:
| 3 |
| 2 |
| 21 |
| 2 |
点评:本题考查的是垂径定理、勾股定理及三角形中位线定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
为了调查全省中学生吃早餐的情况,采用抽样调查方式,在下列抽样方法中,最合理的是( )
| A、抽取几个乡镇的中学生 |
| B、抽取几所城市学校中学生 |
| C、抽取一个地方的所有中学生 |
| D、从每个地方各抽取几个学校的中学生 |
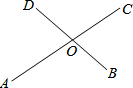 如图,AC、BD是相交的两条线段,O分别为它们的中点.当BD绕点O旋转时,连接AB、BC、CD、DA所得到的四边形ABCD始终为
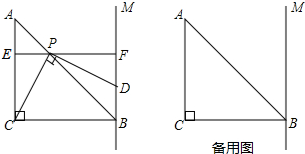
如图,AC、BD是相交的两条线段,O分别为它们的中点.当BD绕点O旋转时,连接AB、BC、CD、DA所得到的四边形ABCD始终为 如图,在等腰Rt△ABC中,∠B=90°,AB=BC=8cm.动点P从点A出发沿线段AB向点B运动,动点Q从点C出发沿射线BC运动,连接PQ,交AC于点D.作PE⊥AC于点E,若在点P,Q运动的过程中,始终保持AP=CQ,则线段DE的长度为
如图,在等腰Rt△ABC中,∠B=90°,AB=BC=8cm.动点P从点A出发沿线段AB向点B运动,动点Q从点C出发沿射线BC运动,连接PQ,交AC于点D.作PE⊥AC于点E,若在点P,Q运动的过程中,始终保持AP=CQ,则线段DE的长度为 如图四边形ABCD中EF∥AD,MN∥AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有
如图四边形ABCD中EF∥AD,MN∥AB,MN与EF交于点P且点P在BD上,图中面积相等的四边形有 如图所示,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上,
如图所示,在△ABC中,∠ACB=90°,AD=AC,BE=BC,D、E两点在AB边上,