题目内容
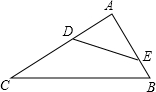如图，∠AED=∠C，DE=4，BC=12，CD=15，AD=3，求AE、BE的长．
分析：先根据已知条件求证△ABC∽△ADE，然后根据相似三角形对应边成比例，代入数值即可求解．
解答：解：∵∠AED=∠C，∠A为公共角，
∴△ABC∽△ADE，∴
=
，
又∵DE=4，BC=12，AC=AD+CD=3+15=18，
∴AE=
=
=6．
∵△ABC∽△ADE，∴
=
，
∴AB=
=
=9，
又∵AB=AE+BE，
∴BE=AB-AE=9-6=3．
答AE的长为6，BE的长为3．
∴△ABC∽△ADE，∴
| DE |
| BC |
| AE |
| AC |
又∵DE=4，BC=12，AC=AD+CD=3+15=18，
∴AE=
| DE•AC |
| BC |
| 4×18 |
| 12 |
∵△ABC∽△ADE，∴
| AD |
| AB |
| AE |
| AC |
∴AB=
| AD•AC |
| AE |
| 3×18 |
| 6 |
又∵AB=AE+BE，
∴BE=AB-AE=9-6=3．
答AE的长为6，BE的长为3．
点评：此题主要考查学生对相似三角形的判定与性质的理解和掌握，解答此题的关键是利用相似三角形对应边成比例．难度不大，是一道基础题．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
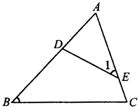12、如图，△AED∽△ABC，其中∠1=∠B，则AD：
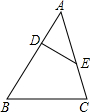已知，如图△ABC∽△AED，AD=5cm，EC=3cm，AC=13cm，则AB=
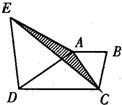20、如图，△AED、△ACB都是等边三角形，画出△ACE以点A为旋转中心，顺时针方向旋转60°后的三角形，并指出∠EAC的对应角，CE的对应线段．
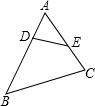如图，