题目内容
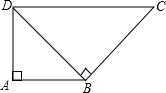由两个等腰直角三角形拼成的四边形（如图），已知
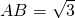，求：
（1）三角形ABD的面积S△ABD；
（2）四边形ABCD的周长．
解：（1）∵三角形ABD是等腰直角三角形，
∴AB=AD=
∴S△ABD=
AB•AD=•×=
（2）∵AB=AD=
∴由勾股定理得：BD=
，
∵三角形CBD是等腰直角三角形，
∴BC=BD=
∴由勾股定理得：CD=2
∴四边形ABCD的周长为：AB+BC+CD+DA=++2+=4+
分析：（1）首先利用等腰直角三角形的AB边的长求得另外一条直角边AD的长，然后即可计算面积．
（2）利用勾股定理求得BD的长，然后再利用勾股定理求得线段CD的长即可求四边形ABCD的周长．
点评：本题考查了等腰直角三角形的性质，充分挖掘等腰直角三角形隐含的条件是解决此题的关键．
∴AB=AD=
∴S△ABD=
AB•AD=•×=（2）∵AB=AD=
∴由勾股定理得：BD=
，∵三角形CBD是等腰直角三角形，
∴BC=BD=
∴由勾股定理得：CD=2
∴四边形ABCD的周长为：AB+BC+CD+DA=
++2+=4+分析：（1）首先利用等腰直角三角形的AB边的长求得另外一条直角边AD的长，然后即可计算面积．
（2）利用勾股定理求得BD的长，然后再利用勾股定理求得线段CD的长即可求四边形ABCD的周长．
点评：本题考查了等腰直角三角形的性质，充分挖掘等腰直角三角形隐含的条件是解决此题的关键．
练习册系列答案
相关题目
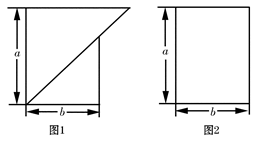
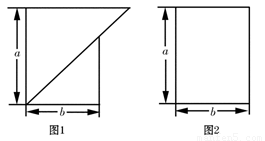
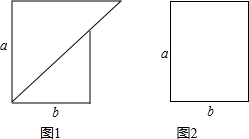有如图所示的两种广告牌，其中图1是由两个等腰直角三角形构成的，图2是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种大小关系用含字母a、b的不等式表示为
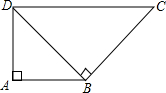由两个等腰直角三角形拼成的四边形（如图），已知AB=
