题目内容
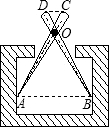如图所示，是一种测量工件内径的仪器，长度相等的两脚AC、BD交叉于点O，且有OA=4OC，OB=4OD．使用时只要将长脚端（AB）伸入工件后，两脚张开，使A、B与内径充分接触，此时量出CD的距离，就可知道该工件内径的大小．请你说明其中包含的道理，并给出具体的合理数值加以验证．
分析：此题属于实际应用题，解此题的关键是将实际问题转化为相似三角形的知识；利用相似三角形的判定与性质解题；相似三角形的对应边成比例；对应边成比例，且对应角相等的三角形相似．
解答：解：∵OA=4OC，OB=4OD，
∴
=
，
且∠AOB=∠COD．
∴△AOB∽△COD．
∴
=
=
．
若CD=2，
则AB=8．
∴
| OA |
| OC |
| OB |
| OD |
且∠AOB=∠COD．
∴△AOB∽△COD．
∴
| CD |
| AB |
| OC |
| OA |
| 1 |
| 4 |
若CD=2，
则AB=8．
点评：本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求解即可，体现了转化的思想．
练习册系列答案
阅读快车系列答案
相关题目
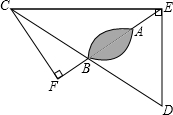（2013•梧州）海上有一小岛，为了测量小岛两端A、B的距离，测量人员设计了一种测量方法，如图所示，已知B点是CD的中点，E是BA延长线上的一点，测得AE=8.3海里，DE=30海里，且DE⊥EC，cos∠D=
在某工厂生产流水线上生产如图所示的零工件，其中∠α称为工件的中心角，生产要求∠α的标准角度为30°±1°，一名质检员在检验时，手拿一量角器逐一测量∠α的度数．请你运用所学的知识分析一下，该名质检员采用的是哪种比较方法？你还能给该质检员设计更好的质检方法吗？请说说你的方法．
如图所示，是一种测量工件内径的仪器，长度相等的两脚AC、BD交叉于点O，且有OA=4OC，OB=4OD．使用时只要将长脚端（AB）伸入工件后，两脚张开，使A、B与内径充分接触，此时量出CD的距离，就可知道该工件内径的大小．请你说明其中包含的道理，并给出具体的合理数值加以验证．