题目内容
新春佳节，电子鞭炮因其安全、无污染开始走俏．某商店经销一种电子鞭炮，已知这种电子鞭炮的成本价为每盒80元，市场调查发现，该种电子鞭炮每天的销售量y（盒）与销售单价x（元）有如下关系：y=﹣2x+320（80≤x≤160）．设这种电子鞭炮每天的销售利润为w元．
（1）求w与x之间的函数关系式；
（2）该种电子鞭炮销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
（3）该商店销售这种电子鞭炮要想每天获得2400元的销售利润，又想买得快．那么销售单价应定为多少元？
-2cos30°+（ 
）-2-|1-
|某种植基地种植一种蔬菜，它的成本是每千克2元，售价是每千克3元，年销量为10 （万千克）．基地准备拿出一定的资金作绿色开发，若每年绿色开发投入的资金为x （万元），该种蔬菜的年销量将是原年销量的n倍，x与n的关系如下表：
x（万元） | 0 | 1 | 2 | 3 | 4 | 5 | … |
m | 1 | 1.5 | 1.8 | 1.9 | 1.8 | 1.5 | … |
（1）猜想n与x之间的函数类型是 函数，求出该函数的表达式并验证；
（2）求年利润W1 （万元） 与绿色开发投入的资金x（万元） 之间的函数关系式（注：年利润W1=销售总额﹣成本费﹣绿色开发投入的资金）；当绿色开发投入的资金不低于3万元，又不超过5万元时，求此时年利润W1 （万元） 的最大值；
（3）若提高种植人员的奖金，发现又增加一部分年销量，经调查发现：再次增加的年销量（万千克） 与每年提高种植人员的奖金z （万元） 之间满足y=﹣z2+4z，若基地将投入5万元用于绿色开发和提高种植人员的奖金，应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入？（
）
B. 
C. 
D. 
在计算器上，按照下图的程序进行操作：
x | -3 | -2 | -1 | 0 | 1 | 2 |
y | -5 | -3 | -1 | 1 | 3 | 5 |
表中的x与y分别是输入的6个数及相应的计算结果：上面操作程序中所按的第三个键和第四个键分别是 ________、________．
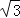C．3 D．6﹣2
