题目内容
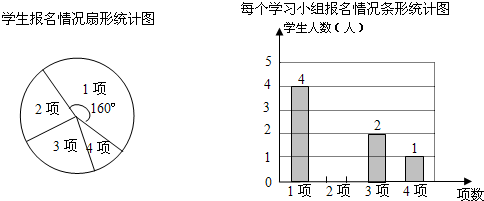
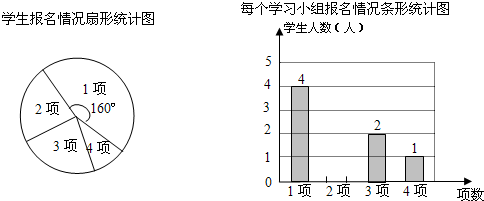
某校八年级每周周一至周五将开展学生“第二课堂”兴趣活动,活动内容有:经典诵读、英语口语训练、校传统体育项目训练、信息技术学习共四项,每一名学生至少报一项.该年级各班学生踊跃报名参加.已知八年级二班有6个学习小组(各组人数相等),各个学习小组报名情况都相同.根据报名情况收集数据,绘制成如下统计图(不完整):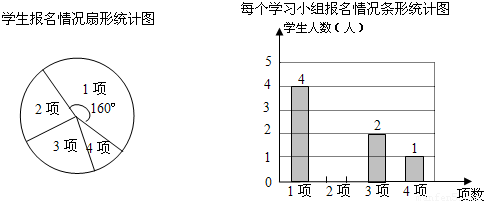
(1)求该班学生人数是多少?并将该条形统计图补充完整;
(2)学校将举行一年一度的“成长杯”学生篮球比赛,该班第一学习小组有2人参加了班级篮球队,他们都只报名参加了最多两项兴趣活动.请你用列表法或树状图的方法求出这两名同学恰好都是只报了1项兴趣活动的学生的概率.
【答案】分析:(1)根据扇形图可得出报1项的圆心角为160°,根据条形图得出报1项的人数为4,可求出该小组人数,进而求出全班人数;
(2)利用树状图得出所有的可能进而求出符合要求的结果,求出概率即可.
解答:解:(1)根据扇形图可得出报1项的圆心角为160°,根据条形图得出报1项的人数为4,
故该小组人数为:4÷ =9(人),
=9(人),
故报两项的人数为:9-4-2-1=2(人),
∵八年级二班有6个学习小组(各组人数相等),
∴该班学生人数是:6×9=54人,如图所示:
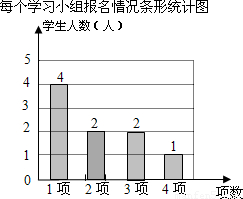 ;
;
(2)设报一项项目的分别为:A1,B1,C1,D1,报两项的为:A2,B2.

所有的结果为:30种,这两名同学恰好都是只报了1项兴趣活动的学生的情况为12种,故这两名同学恰好都是只报了1项兴趣活动的学生的概率为: =
= .
.
点评:本题考查了扇形统计图及条形统计图的知识以及树状图法求概率,解题的关键是从统计图中求出每小组的人数.
(2)利用树状图得出所有的可能进而求出符合要求的结果,求出概率即可.
解答:解:(1)根据扇形图可得出报1项的圆心角为160°,根据条形图得出报1项的人数为4,
故该小组人数为:4÷
 =9(人),
=9(人),故报两项的人数为:9-4-2-1=2(人),
∵八年级二班有6个学习小组(各组人数相等),
∴该班学生人数是:6×9=54人,如图所示:
 ;
;(2)设报一项项目的分别为:A1,B1,C1,D1,报两项的为:A2,B2.

所有的结果为:30种,这两名同学恰好都是只报了1项兴趣活动的学生的情况为12种,故这两名同学恰好都是只报了1项兴趣活动的学生的概率为:
 =
= .
.点评:本题考查了扇形统计图及条形统计图的知识以及树状图法求概率,解题的关键是从统计图中求出每小组的人数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目