题目内容
 如图所示的几何体是由若干个相同的小正方体搭建而成的(第一层,1个;第二层3个;第3层,6个),小正方体的一个侧面的面积为1.今要用红颜色给这个几何体的表面着色(但底部不着色),要着色的面积是多少?
如图所示的几何体是由若干个相同的小正方体搭建而成的(第一层,1个;第二层3个;第3层,6个),小正方体的一个侧面的面积为1.今要用红颜色给这个几何体的表面着色(但底部不着色),要着色的面积是多少?分析:数出第一层着色的个正方形、第二层着色的正方形、第三层着色的正方形,求出共有几个正方形,即可求出答案.
解答:解:∵第一层着色的有5个正方形,
第二层着色的有10个正方形,
第三层着色的有15个正方形,
∴共着色的有5+10+15=30,
∵小正方体的一个侧面的面积为1,
∴30×1=30,
答:此几何体要着色的面积是30.
第二层着色的有10个正方形,
第三层着色的有15个正方形,
∴共着色的有5+10+15=30,
∵小正方体的一个侧面的面积为1,
∴30×1=30,
答:此几何体要着色的面积是30.
点评:本题考查了有关几何体的表面积的计算问题,主要考查学生的观察图形的能力和计算能力,题目比较典型,难度适中.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 如图所示的几何体是由一些小立方块搭成的,则这个几何体的左视图是( )
如图所示的几何体是由一些小立方块搭成的,则这个几何体的左视图是( )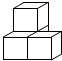 如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图为( )
如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图为( )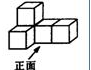 如图所示的几何体是由五个小正方体搭成的,它的左视图是( )
如图所示的几何体是由五个小正方体搭成的,它的左视图是( ) 如图所示的几何体是由一些棱长为1个单位的小正方体搭成的,仔细观察几何体,一共有
如图所示的几何体是由一些棱长为1个单位的小正方体搭成的,仔细观察几何体,一共有