Question

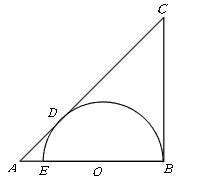
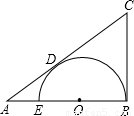
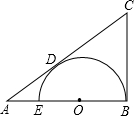如图EB是⊙O的直径，A是BE的延长线上一点，过A作⊙O的切线AC，切点为D，过B作⊙O的切线BC，交AC于点C，若EB=BC=6，求：AD，AE的长．

Answer 1

分析：连接OD；设AE=x，根据切割线定理和勾股定理列方程求得x的值，再进一步求得AD的长．

解答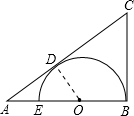：解：连接OD，则∠ADO=90°；
又∵∠ABC=90°，∠A=∠A；
∴△ADO∽△ABC；
∴

AD

AB

=

OD

BC

；
设AE=x，则有：

AD

x+6

=

3

6

=

1

2

，AD=

x+6

2

；
又∵AD²=x（x+6），∴

(x+6)2

4

=x(x+6)；
整理，得：x²+4x-12=0；
∴x=2，x=-6（舍）；
即：AE=2，AD=

2(2+6)

=4．

点评：解决此题的关键是能够综合运用切割线定理和勾股定理列方程求解．