题目内容
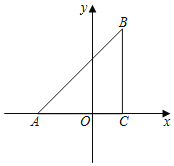
【题目】如图，在平面直角坐标系中，点A的坐标为(0，4)，点B的坐标为(4，4)，点C的坐标为(4，0)，点D是x轴上(在点O右侧)任意一点，以AD为边向右侧作正方形ADEF，连接BF，设点D的坐标为(t，0)处.
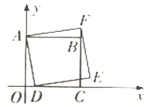
(1)求证：△AOD≌△ABF；
(2)求点E的坐标(用含有t的代数式来表示)；
(3)当△DBE是等腰三角形时，请直接写出t的值.
【答案】(1) 见解析；(2) E(4+t,t) (3) 2,4,8.
【解析】
（1）由四边形ABCO和ADFE是正方形，得∠AOD=∠ABF=90°，AO=AB=4，AD=AF，即可利用HL证明△AOD≌△ABF；
（2）过点E作EH⊥x轴于点H，然后证明△AOD≌△DHE，得到DH=OA=4，OD=EH=t，即可得到点E的坐标；
（3）由（2）知点D为（t，0），点B为（4，4），点E为（4+t，t），利用勾股定理求出BD、BE、DE的长度，由△DBE是等腰三角形时，可分为三种情况进行讨论，即当BD=DE，BD=BE，DE=BE时，求出t的值即可.
（1）证明：根据题意，OA=OC=AB=BC=4，∠AOC=90°，
∴四边形ABCO是正方形，
∴∠AOC=∠ABF=90°，
∵四边形ADEF是正方形，
∴AD=AF，
∴△AOD≌△ABF（HL）；
（2）解：如图：过点E作EH⊥x轴于点H，
∵∠AOD=∠ADE=90°，
∴∠OAD+∠ADO=∠EDH+∠ADO=90°，
∴∠OAD=∠EDH，
∵AD=DE，∠AOD=∠DHE=90°，
∴△AOD≌△DHE（AAS），
∴AO=DH=4，OD=EH=t，
∴OH=4+t，
∴点E的坐标为：（4+t，t）；
（3）由（2）可知，点D为（t，0），点B为（4，4），点E为（4+t，t），
∴
，
，
，
∵△DBE是等腰三角形，
当BD=DE时，有
，
解得：
；
当BD=BE时，有
，
解得：
或
（舍去）；
当DE=BE时，有
，
解得：
或
（舍去）；
∴当，4或8时，△DBE是等腰三角形.
