题目内容
如图,A,B,C三点在⊙O上,且AB是⊙O的直径,半径OD⊥AC,垂足为F,若∠A=30º,OF=3,则OA= ,AC= .

【答案】
6, 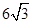 .
.
【解析】
试题分析:先根据直角三角形的性质求出OA的长,故可得出AB的长,再根据圆周角定理求出∠ACB的度数,由直角三角形的性质求出AB的长,在Rt△ABC中由勾股定理即可求出AC的长,∵OD⊥AC,∠A=30°,OF=3,
∴∠AFO=90°,∴OA=2OF=2×3=6,∴AB=2OA=2×6=12,∵AB是⊙O的直径,∴∠ACB=90°,∴BC=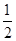 AB=
AB=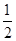
×12=6,在Rt△ABC中,∵AB=12,BC=6,∴AC2=AB2−BC2=108, AC=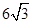 .
.
考点:1.圆周角定理;2.含30度角的直角三角形;3.垂径定理.

练习册系列答案
相关题目
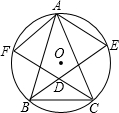 如图,⊙O上三点A、B、C,AB=AC,∠ABC的平分线交⊙O于点E,∠ACB的平分线交⊙O于点F,BE和CF相交于点D,四边形AFDE是菱形吗?验证你的结论.
如图,⊙O上三点A、B、C,AB=AC,∠ABC的平分线交⊙O于点E,∠ACB的平分线交⊙O于点F,BE和CF相交于点D,四边形AFDE是菱形吗?验证你的结论. 如图,方格有三点分别是A(3,8),B(1,6)C(5,6).
如图,方格有三点分别是A(3,8),B(1,6)C(5,6). 如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD=
如图,△ABC的三点都在⊙O上,AB是直径,∠BAD=50°,则∠ACD= 如图,⊙O上三点A、B、C把圆分成
如图,⊙O上三点A、B、C把圆分成
 如图,数轴上三点所对应的数为a,b,c,则下列关系式中错误的是( )
如图,数轴上三点所对应的数为a,b,c,则下列关系式中错误的是( )