题目内容
【题目】如图,在菱形ABCD中,∠A=60°,点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.

(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证:BM⊥FM.
【答案】(1)1;(2)证明见解析.
【解析】
试题分析:(1)根据已知和菱形的性质证明△CBE≌△CDF,得到BE=DF,证明△AEF是等边三角形,求出EF的长;
(2)延长BM交DC于点N,连结FN,证明△CMN≌△EMB,得到NM=MB,证明△FDN≌△BEF,得到FN=FB,得到BM⊥MF.
试题解析:(1)∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠D=∠CBE,
又∵∠BCE=∠DCF,
在△CBE与△CDF中,
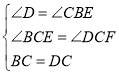 ,
,
∴△CBE≌△CDF,
∴BE=DF.
又∵AB=AD,
∴AB-BE=AD-DF,即AE=AF,
又∵∠A=60°,
∴△AEF是等边三角形,
∴EF=AF,
∵AF=1,
∴EF=1.
(2)如图1,延长BM交DC于点N,连结FN,
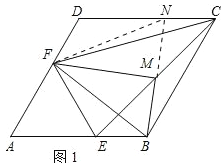
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
在△CMN与△EMB中,
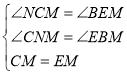 ,
,
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.
∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,
∴∠A+∠D=180°,
又∵∠A=60°,
∴∠D=120°,
∴∠D=∠BEF.
在△FDN与△BEF中,
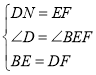 ,
,
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,
∴BM⊥MF

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目