题目内容
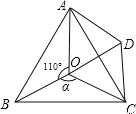
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
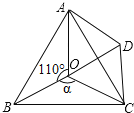
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
【答案】(1)证明见解析;(2)当α=150°时,△AOD是直角三角形,理由见解析;(3)当α的度数为125°或110°或140°时,△AOD是等腰三角形.
【解析】试题分析:(1)根据旋转的性质可得出![]() ,结合题意即可证得结论;
,结合题意即可证得结论;
(2)结合(1)的结论可作出判断;
(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
试题解析:(1)证明:∵将△BOC绕点C按顺时针方向旋转![]() 得△ADC,
得△ADC,
∴CO=CD,∠OCD=![]() ,
,
∴△COD是等边三角形,
(2)当![]() 时,△AOD是直角三角形.
时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60![]() 得△ADC,
得△ADC,
∴△BOC≌△ADC,
![]()
又∵△COD是等边三角形,
∴∠ODC=![]() ,
,
![]()
![]()
![]()
∴△AOD不是等腰直角三角形,即△AOD是直角三角形。
(3)①要使AO=AD,需∠AOD=∠ADO,
![]()
![]()
![]()
②要使OA=OD,需∠OAD=∠ADO.
![]()
![]()
![]()
③要使OD=AD,需∠OAD=∠AOD.
![]()
![]()
![]()
解得![]()
综上所述:当α的度数为![]() 或
或![]() 或
或![]() 时,△AOD是等腰三角形。
时,△AOD是等腰三角形。

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.