题目内容
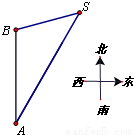
(2011四川泸州,25,7分)如图,一艘船以每小时60海里的速度自A向正北方向航行,船在A处时,灯塔S在船的北偏东30°,航行1小时后到B处,此时灯塔S在船的北偏东75°,(运算结果保留根号)
(1)求船在B处时与灯塔S的距离;
(2)若船从B处继续向正北方向航行,问经过多长时间船与灯塔S的距离最近.
【答案】
解:(1)延长AB,作SC⊥AC,垂足为C.设SC=x.
在Rt△ASC中,AC=xcot30°=
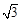 x;在Rt△BSC中,BC=xcot75°=(2-
x;在Rt△BSC中,BC=xcot75°=(2-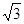 )x.
)x.
∵AB=60海里,又∵AB=AC-BC= 3x-(2-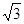 )x=(2
)x=(2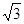 -2)x,
-2)x,
∴(2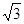 -2)x=60,解得:x=15(
-2)x=60,解得:x=15(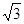 +1)海里.BS= xsin75°=30
+1)海里.BS= xsin75°=30 海里.
海里.
故(1)BS=30 海里;
海里;
(2)船与灯塔S的最近距离为CS,船的航行时间为 小时.
小时.
【解析】略

练习册系列答案
相关题目
 ,其中 x=
,其中 x= .
.
 的图象在第一、三象限,则m的取值范围是
.
的图象在第一、三象限,则m的取值范围是
. +(sin30°)-1+|-2|.
+(sin30°)-1+|-2|.