题目内容
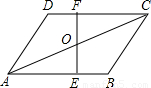
（2010•德宏州）如图，在平行四边形ABCD中，O是其对角线AC的中点，EF过点O．（1）求证：∠OEA=∠OFC；
（2）求证：BE=DF．
【答案】分析：（1）由?ABCD得到CD=AB，CD∥AB，推出△COF和△AOE全等，即可推出结论；
（2）由（1）得到AB=CD，AE=CF，相减即可得到答案．
解答：证明：（1）∵四边形ABCD 是平行四边形，
∴CD=AB，CD∥AB，
∴∠DCA=∠BAC，
∵OA=OC，
∴△COF≌△AOE，
∴∠OEA=∠OFC．
（2）由（1）知：△COF≌△AOE，CD=AB，
∴AE=CF，
∴BE=DF．
点评：本题主要考查了平行四边形的性质，全等三角形的性质和判定等知识点，解此题的关键是证明△COF和△AOE全等．
（2）由（1）得到AB=CD，AE=CF，相减即可得到答案．
解答：证明：（1）∵四边形ABCD 是平行四边形，
∴CD=AB，CD∥AB，
∴∠DCA=∠BAC，
∵OA=OC，
∴△COF≌△AOE，
∴∠OEA=∠OFC．
（2）由（1）知：△COF≌△AOE，CD=AB，
∴AE=CF，
∴BE=DF．
点评：本题主要考查了平行四边形的性质，全等三角形的性质和判定等知识点，解此题的关键是证明△COF和△AOE全等．
练习册系列答案
导学教程高中新课标系列答案
相关题目