题目内容
【题目】已知：如图，D是△ABC的边上一点，M是AC的中点，CN∥AB交DM的延长线于N，且AB=10，BC=8,AC=7.
(1)求证：四边形ADCN是平行四边形；
（2）当AD为何值时，四边形ADCN是矩形。
【答案】（1）证明见解析；（2）当AD为
时，四边形ADCN是矩形
【解析】分析：分析：（1）根据平行四边形的判定定理得出即可；（2）由矩形的性质得到CD⊥AB，在RT△ACD中，由
,求出AD即可.
（1）证明：①∵CN∥AB，∴∠DAC=∠NCA，
∵在△AMD和△CMN中，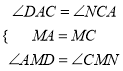 
，
∴△AMD≌△CMN（ASA）， ∴AD=CN，
又∵AD∥CN， ∴四边形ADCN是平行四边形，
（2）若四边形ADCN是矩形，∴CD⊥AB
设AD=x，则CD2=49－x2=64－（10－x）2 ,
100－20x=15，x=
，∴AD=
.
练习册系列答案
相关题目
