Question

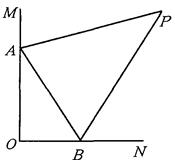
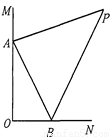
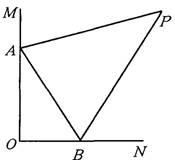
如图，∠MON＝90°，AP平分∠MAB，BP平分∠ABN．

（1）求∠P的度数；

（2）若∠MON＝80°，其余条件不变，求∠P的度数；

（3）经过（1）、（2）的计算，猜想并证明∠MON与∠P的关系．

 

Answer 1

（1）45°（2）50°（3）∠MON+2∠P=180°

解析:（1）∵∠BAM=∠AOB+∠ABO      ∠ABN=∠AOB+∠BAO

∴∠BAM+∠ABN=∠AOB+∠ABO+∠AOB+∠BAO=180°+ 90°=270°………  1分

∵AP平分∠MAB，BP平分∠ABN

∴∠BAP= ∠BAM，∠ABP= ∠ABN

∴∠BAP+∠ABP= （∠BAM+∠ABN）=135°

在△ABP中   ∠BAP+∠ABP+∠P=180°

∴∠P=180°- 135°=45°；         ……………………  2分

（2）∵∠BAM=∠AOB+∠ABO     ∠ABN=∠AOB+∠BAO

∴∠BAM+∠ABN=∠AOB+∠ABO+∠AOB+∠BAO=180°+ 80°=260°…  3分

∵AP平分∠MAB，BP平分∠ABN

∴∠BAP= ∠BAM，∠ABP= ∠ABN

∴∠BAP+∠ABP= （∠BAM+∠ABN）=130°

在△ABP中   ∠BAP+∠ABP+∠P=180°

∴∠P=180°- 130°= 50°；        …………………… 4分

（3）∠MON+2∠P=180°

∵∠BAM=∠MON+∠ABO   ∠ABN=∠MON+∠BAO

∴∠BAM+∠ABN=∠MON+∠ABO+∠MON+∠BAO =180°+∠MON     ……  5分

∵AP平分∠MAB，BP平分∠ABN

∴∠BAP= ∠BAM，∠ABP= ∠ABN

∴∠BAP+∠ABP= （∠BAM+∠ABN）= （180°+∠MON）

在△ABP中   ∠BAP+∠ABP+∠P=180°

 （180°+∠MON）+∠P=180°  ∴∠MON+2∠P=180°．

（1）利用外角性质，求得∠BAM+∠ABN=270°；由AP平分∠MAB，BP平分∠ABN．∴∠BAP+∠ABP= （∠BAM+∠ABN）=135°，由三角形内角和定理，∴∠P=180°-135°=45°；

（2）与问题（1）的思路相同；

（3）利用外角性质，求得∠BAM+∠ABN=∠MON+∠ABO+∠MON+∠BAO=（∠MON+∠ABO+∠BAO）+∠MON=180°+∠MON；由AP平分∠MAB，BP平分∠ABN．求∠BAP+∠ABP，由三角形内角和定理，∠BAP+∠ABP+∠P=180°从而求所求的度数