题目内容
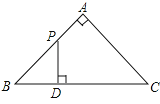
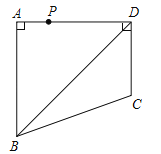
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=![]() ,CD=
,CD=![]() ,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为
,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为![]() ,则满足条件的点P有 个.
,则满足条件的点P有 个.
【答案】2.
【解析】
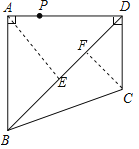
试题分析:首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF的长为![]() ,比较得出答案.
,比较得出答案.
试题解析:过点A作AE⊥BD于E,过点C作CF⊥BD于F,∵∠BAD=∠ADC=90°,AB=AD=![]() ,CD=
,CD=![]() ,∴∠ABD=∠ADB=45°,∴∠CDF=90°﹣∠ADB=45°,∵sin∠ABD=
,∴∠ABD=∠ADB=45°,∴∠CDF=90°﹣∠ADB=45°,∵sin∠ABD=![]() ,∴AE=ABsin∠ABD=
,∴AE=ABsin∠ABD=![]() sin45°=3>
sin45°=3>![]() ,CF=2<
,CF=2<![]() ,所以在AB和AD边上有符合P到BD的距离为
,所以在AB和AD边上有符合P到BD的距离为![]() 的点2个,故答案为:2.
的点2个,故答案为:2.

练习册系列答案
相关题目