��Ŀ����
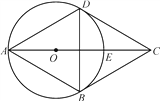
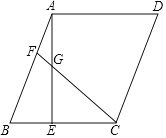
����Ŀ����ͼ�� ABCD �ĶԽ��� AC �� BD �ཻ�ڵ�O �� BD 12cm �� AC 6cm ���� E ���߶� BO �ϴӵ� B ��1cm / s ���ٶ���� O �˶����� F ���߶�OD �ϴӵ�O �� 2cm / s ���ٶ���� D �˶���
��1������ E ��F ͬʱ�˶������˶�ʱ��Ϊt �룬��t Ϊ��ֵʱ���ı��� AECF ��ƽ���ı��Σ�
��2���ڣ�1���������£��� AB Ϊ��ֵʱ�� AECF �����Σ�
��3����2�������� AECF �������

���𰸡���1��t��2s����2��AB=![]() ����3��24.
����3��24.
��������
��1������ƽ���ı��Σ�����6t��2t���������tֵ��
��2���������Σ���AC��ֱ��BD������AO2��BO2��AB2����AB����
��3���ɣ�1����2����֪��t��2s��AB=![]() ʱ���ı���AECF�����Σ����EF��8�����ǵõ����ۣ�
ʱ���ı���AECF�����Σ����EF��8�����ǵõ����ۣ�
�⣺��1�����ı���ABCDΪƽ���ı��Σ�
��AO��OC��EO��OF��
��BO��OD��6cm��
��EO��6t��OF��2t��
��6t��2t��
��t��2s��
�൱tΪ2��ʱ���ı���AECF��ƽ���ı��Σ�
��2�����ı���AECF�����Σ���AC��BD��
��AO2��BO2��AB2��
��AB��![]() ��
��![]() ��
��
�൱ABΪ![]() ʱ��AECF�����Σ�
ʱ��AECF�����Σ�
��3���ɣ�1����2����֪��t��2s��AB=![]() ʱ���ı���AECF�����Σ�
ʱ���ı���AECF�����Σ�
��EO��6t=4��
��EF=8��
������AECF�������![]() ��
��

����Ŀ��Ϊ�˱���������ij�������ۺ�����ָ�Ӳ���������A��B�����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����A�ͺŵ���ˮ�����豸��̨������75��Ԫ����B�ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
��ˮ�����豸 | A�� | B�� |
�۸���Ԫ/̨�� | m | m-3 |
�´�����ˮ������/̨�� | 220 | 180 |
��1����m��ֵ��
��2���������ʽ����ƣ�ָ�Ӳ����ڹ�����ˮ�����豸���ʽ���165��Ԫ�����ж����ֹ����������ÿ����ദ����ˮ���Ķ�����