题目内容
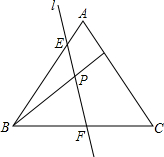 如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°
如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°(1)写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)探究:当BD什么条件时(其它条件不变),PF=
| 1 | 2 |
分析:(1)△BPF∽△EBF与△BPF∽△BCD这两组三角形都可由一个公共角和一组60°角来证得.
(2)先看PF=
PE能得出什么结论.根据△BPF∽△EBF,可得BF2=PF•EF=3PF2,因此BF=
PF,且∠BPF=60°,∵∠PFB=90°,∴∠PBF=90-60=30°,因此当BD平分∠ABC时,PF=
PE.
(2)先看PF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
解答:(1)答:△BPF∽△EBF与△BPF∽△BCD.
以△BPF∽△EBF为例,
证明:∵∠BPF=∠EBF=60°,∠BFP=∠BFE,
∴△BPF∽△EBF;
(2)答:BD平分∠ABC时,PF=
PE.
证明:∵BD平分∠ABC,
∴∠ABP=∠PBF=30°.
∵∠BPF=60°,
∴∠BFP=90°.
∴PF=
PB.
又∵∠BEP=∠BPF-∠EBP=60°-30°=30°=∠ABP,
∴BP=EP,
∴PF=
PE.
以△BPF∽△EBF为例,
证明:∵∠BPF=∠EBF=60°,∠BFP=∠BFE,
∴△BPF∽△EBF;
(2)答:BD平分∠ABC时,PF=
| 1 |
| 2 |
证明:∵BD平分∠ABC,
∴∠ABP=∠PBF=30°.
∵∠BPF=60°,
∴∠BFP=90°.
∴PF=
| 1 |
| 2 |
又∵∠BEP=∠BPF-∠EBP=60°-30°=30°=∠ABP,
∴BP=EP,
∴PF=
| 1 |
| 2 |
点评:本题主要考查了等边三角形的性质、相似三角形的判定和性质、直角三角形的判定和性质等知识点.

练习册系列答案
相关题目
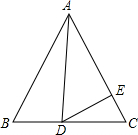 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: