题目内容
已知a、b、c的平均值为5，X、Y、Z的平均值为7，则2a+3X，2b+3Y，2c+3Z的平均值为
- A.31
- B.
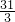
- C.
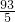
- D.17
A
分析：首先求得a、b、c与X、Y、Z的和，然后计算2a+2b+2c与3X+3Y+3Z的值，最后求平均数即可．
解答：∵a、b、c的平均值为5，X、Y、Z的平均值为7，
∴a+b+c=15，X+Y+Z=21，
∴2a+2b+2c=30，3X+3Y+3Z=63
∴（2a+3X）+（2b+3Y）+（2c+3Z）=2a+2b+2c+3X+3Y+3Z=93
∴2a+3X，2b+3Y，2c+3Z的平均值为93÷3=31，
故选A．
点评：本题考查了算术平均数的变化，分别求得两组数的和是求解本题的关键．
分析：首先求得a、b、c与X、Y、Z的和，然后计算2a+2b+2c与3X+3Y+3Z的值，最后求平均数即可．
解答：∵a、b、c的平均值为5，X、Y、Z的平均值为7，
∴a+b+c=15，X+Y+Z=21，
∴2a+2b+2c=30，3X+3Y+3Z=63
∴（2a+3X）+（2b+3Y）+（2c+3Z）=2a+2b+2c+3X+3Y+3Z=93
∴2a+3X，2b+3Y，2c+3Z的平均值为93÷3=31，
故选A．
点评：本题考查了算术平均数的变化，分别求得两组数的和是求解本题的关键．
练习册系列答案
相关题目
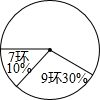在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 3 | 2 |
（2）已知乙运动员10次射击的平均成绩为9环，方差为1.2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由．（参考资料：S2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |