Question

动手操作（本小题满分7分）

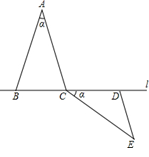
如图在△ABC和△CDE中，AB=AC=CE，BC=DC=DE，AB>BC，∠BAC=∠DCE=∠，点B、C、D在直线l上，按下列要求画图（保留画图痕迹）；

（1）画出点E关于直线l的对称点E’，连接CE’ 、DE’；

（2）以点C为旋转中心，将（1）中所得△CDE’ 按逆时针方向旋转，使得CE’与CA重合，

得到△CD’E’’（A）．画出△CD’E’’（A）．解决下面问题：

①线段AB和线段CD’的位置关系是   ▲  ；理由是：      ▲       ．

②求∠的度数．

 

Answer 1

【答案】

（1）画出对称点（2）①   平行②36°

【解析】（1）画出对称点                          

（2）画出△CD’E’’                            

①   平行  ；    理由：（略） 

②∵四边形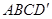是等腰梯形，

∴∠ABC=∠D’AB=2∠D’CB=2∠         

∵AB=AC∴∠ABC=∠ACB=2∠          

在△ABC中，∠A+∠ABC+∠ACB =180°

求得∠=36°                          

根据对称和旋转的性质作图，求解