题目内容
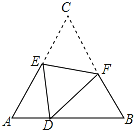
【题目】如图，D是等边△ABC边AB上的一点，且AD=1，BD=2，现将△ABC折叠，使点C与D重合，折痕EF，点E、F分别在AC和BC上，若BF=1.2，则CE=（ ）
A．
B．
C．
D．
【答案】B
【解析】
试题分析：先求得AC=AB=3，由翻折的性质可知：EC=ED，然后证明△AED∽△BDF，利用相似三角形的性质可求得AE=
，然后可求得CE的长．
解：∵△ABC为等边三角形，
∴AC=AB=3，∠A=∠B=∠C=60°．
由翻折的性质可知：∠EDF=60°．
∴∠FDB+∠EDA=120°．
∵∠EDA+∠AED=120°，
∴∠AED=∠FDB．
∴△AED∽△BDF．
∴
，即
．
解得：AE=．
CE=3﹣AE=3﹣=
．
故选：B．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
