Question

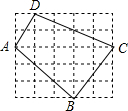
如图是由边长为1的小正方形组成的网格
（1）求四边形ABCD的面积；
（2）判断AD与CD的位置关系，并说明理由．

Answer 1

分析：（1）根据四边形ABCD的面积=大正方形的面积-四个小直角三角形的面积计算即可；
（2）AD⊥DC，利用勾股定理的逆定理证明△ADC是直角三角形即可．

解答：解：（1）由题意可知四边形ABCD的面积=大正方形的面积-四个小直角三角形的面积=5×5-

1

2

×1×2-

1

2

×4×2-

1

2

×3×3-

1

2

×2×3=

25

2

；
（2）AD⊥CD，理由如下：
∵AD=

12+22

=

5

，DC=

22+42

=

20

，AC=5，
∴AD²+DC²=AC²=25，
∴△ADC是直角三角形，
∴AD⊥CD，

点评：本题考查了三角形的面积公式和勾股定理的逆定理的运用．