题目内容
有四张卡片（背面完全相同），分别写有数字1、2、﹣1、﹣2，把它们背面朝上洗匀后，甲同学抽取一张记下这个数字后放回洗匀，乙同学再从中抽出一张，记下这个数字，用字母b、c分别表示甲、乙两同学抽出的数字．
（1）用列表法求关于x的方程x2+bx+c=0有实数解的概率；
（2）求（1）中方程有两个相等实数解的概率．
（1）用列表法求关于x的方程x2+bx+c=0有实数解的概率；
（2）求（1）中方程有两个相等实数解的概率．
：解：（1）列表得：
∴一共有16种等可能的结果，
∵关于x的方程x2+bx+c=0有实数解，即 b2﹣4c≥0，
∴关于x的方程x2+bx+c=0有实数解的有（1，﹣1），（1，﹣2），（2，1），（2，﹣1），（2，﹣2），（﹣1，﹣1），（﹣1，﹣2），（﹣2，1），（﹣2，﹣1），（﹣2，﹣2）共10种情况，
∴关于x的方程x2+bx+c=0有实数解的概率为：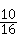
=
；
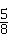（2）（1）中方程有两个相等实数解的有（﹣2，1），（2，1），
∴（1）中方程有两个相等实数解的概率为：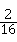
=
．
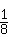| （1，﹣2） | （2，﹣2） | （﹣1，﹣2） | （﹣2，﹣2） |
| （1，﹣1） | （2，﹣1） | （﹣1，﹣1） | （﹣2，﹣1） |
| （1，2） | （2，2） | （﹣1，2） | （﹣2，2） |
| （1，1） | （2，1） | （﹣1，1） | （﹣2，1） |
∵关于x的方程x2+bx+c=0有实数解，即 b2﹣4c≥0，
∴关于x的方程x2+bx+c=0有实数解的有（1，﹣1），（1，﹣2），（2，1），（2，﹣1），（2，﹣2），（﹣1，﹣1），（﹣1，﹣2），（﹣2，1），（﹣2，﹣1），（﹣2，﹣2）共10种情况，
∴关于x的方程x2+bx+c=0有实数解的概率为：
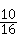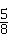=；（2）（1）中方程有两个相等实数解的有（﹣2，1），（2，1），
∴（1）中方程有两个相等实数解的概率为：
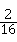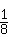=．：（1）根据题意列表，然后根据表格求得所有等可能的结果与关于x的方程x2+bx+c=0有实数解的情况数，根据即可概率公式求解；
（2）首先求得（1）中方程有两个相等实数解的情况，然后即可根据概率公式求解．
（2）首先求得（1）中方程有两个相等实数解的情况，然后即可根据概率公式求解．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
的黄球，还有红球和白球，除此以外没其他颜色的球，只知道红球和白球的数量相差很大，现在不能倒出来一个个数，你能有办法估计哪种颜色的球可能最多？说说你的方法．
选手的所有可能的结论； (2). （3分）对于选手
校园手机”现象越来越受到社会的关注．“寒假”期间，记者刘凯随机调查了某区若干名学生和家长对中学生带手机现
象的看法，统计整理并制作了如下的统计图：
