题目内容
阅读理解:对于三个数a,b,c用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
=
,min{-1,2,3}=-1,min{-1,2,a}=

问题解决:
(1)填空:min{-5,-
,-
}=
如果min{2,2x+2,4-2x}=2,则x的取值范围为
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x.
②根据①你发现了结论“如果M{a,b,c}=min{a,b,c},那么
③运用②的结论,填空:
若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=
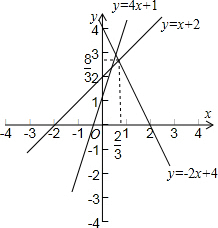
(3)在如图所示的同一直角坐标系中作出函数y=4x+1,y=x+2,y=-2x+4的图象.通过观察图象,填空:min{4x+1,x+2,-2x+4}的最大值为
.
| -1+2+3 |
| 3 |
| 4 |
| 3 |
|

问题解决:
(1)填空:min{-5,-
| 26 |
| 1 |
| 2 |
-
| 26 |
-
;| 26 |
如果min{2,2x+2,4-2x}=2,则x的取值范围为
0
0
≤x≤1
1
.(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x.
②根据①你发现了结论“如果M{a,b,c}=min{a,b,c},那么
a=b=c
a=b=c
(填a,b,c的大小关系)”.证明你发现的结论.③运用②的结论,填空:
若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=
-4
-4
.(3)在如图所示的同一直角坐标系中作出函数y=4x+1,y=x+2,y=-2x+4的图象.通过观察图象,填空:min{4x+1,x+2,-2x+4}的最大值为
| 8 |
| 3 |
| 8 |
| 3 |
分析:(1)min{-5,-
,-
}就是括号内的三个数中的最小的一个,据此即可确定;
min{2,2x+2,4-2x}=2,则2x+2≥2,且4-2x≥2,两个式子同时成立,据此即可求得x的范围;
(2)①M{2,x+1,2x}=
=x+1,若M{2,x+1,2x}=min{2,x+1,2x},则x+1是2、x+1、2x中最小的一个,即:x+1≤2且x+1≤2x,据此即可求得x的值;
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
(3)首先作出三个函数的图象,min{4x+1,x+2,-2x+4}的最大值为三个函数的图象的交点中,横坐标最大的点的纵坐标就是所求的值.
| 26 |
| 1 |
| 2 |
min{2,2x+2,4-2x}=2,则2x+2≥2,且4-2x≥2,两个式子同时成立,据此即可求得x的范围;
(2)①M{2,x+1,2x}=
| 2+x+1+2x |
| 3 |
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
(3)首先作出三个函数的图象,min{4x+1,x+2,-2x+4}的最大值为三个函数的图象的交点中,横坐标最大的点的纵坐标就是所求的值.
解答:解(1)-
;0≤x≤1.
(2)①∵M{2,x+1,2x}=
=x+1.
∵2x-(x+1)=x-1.
当x≥1时,则min{2,x+1,2x}=2,则x+1=2,∴x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,∴x=1(舍去)
综上所述:x=1.
②a=b=c.理由如下:
∵M{a,b,c}=
,
如果min{a,b,c}=c,则a≥c,b≥c.
则有
=c,即a+b-2c=0.
∴(a-c)+(b-c)=0.
又a-c≥0,b-c≥0,∴a-c=0,且b-c=0.
∴a=b=c.
其他情况同理可证,故a=b=c.
③根据题意得:
,
解得:
则x+y=-3-1=-4.
(3)作出图象(如图所示),由图象知min{4x+1,x+2,-2x+4}的最大值为
.
| 26 |
(2)①∵M{2,x+1,2x}=
| 2+x+1+2x |
| 3 |
∵2x-(x+1)=x-1.
当x≥1时,则min{2,x+1,2x}=2,则x+1=2,∴x=1.
当x<1时,则min{2,x+1,2x}=2x,则x+1=2x,∴x=1(舍去)
综上所述:x=1.
②a=b=c.理由如下:
∵M{a,b,c}=
| a+b+c |
| 3 |
如果min{a,b,c}=c,则a≥c,b≥c.
则有
| a+b+c |
| 3 |
∴(a-c)+(b-c)=0.
又a-c≥0,b-c≥0,∴a-c=0,且b-c=0.
∴a=b=c.
其他情况同理可证,故a=b=c.
③根据题意得:
|
解得:
|
则x+y=-3-1=-4.
(3)作出图象(如图所示),由图象知min{4x+1,x+2,-2x+4}的最大值为
| 8 |
| 3 |

点评:本题是一次函数与平均数,最小值函数相结合的题目,正确理解(1)中得到的结论是关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
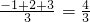 ,min{-1,2,3}=-1,min{-1,2,a}=
,min{-1,2,3}=-1,min{-1,2,a}=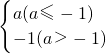

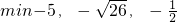 =______;
=______;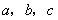 ,用
,用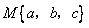 表示这三个数的平均数,用
表示这三个数的平均数,用 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: ;
;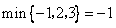 ;
;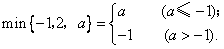 解决下列问题:
解决下列问题: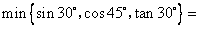 ______;
______;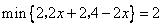 ,则x的取值范围为
,则x的取值范围为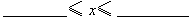 .
. ,求x;
,求x; 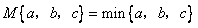 ,那么______ (填
,那么______ (填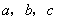 的大小关系)”.证明你发现的结论;
的大小关系)”.证明你发现的结论; 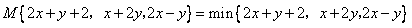 ,则
,则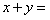 ______ .
______ .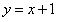 ,
,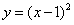 ,
,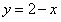 的图象(不需列表描点).通过观察图象,
的图象(不需列表描点).通过观察图象, 的最大值为______ .
的最大值为______ .