题目内容
下列多边形一定相似的为( )
| A.两个三角形 | B.两个四边形 | C.两个正方形 | D.两个平行四边形 |
C.
解析试题分析:要判断两个多边形是否相似,需要看对应角是否相等,对应边的比是否相等.
三角形、四边形、平行四边形都属于形状不唯一确定的图形,即对应角、对应边的比不一定相等,故不一定相似,A、B、D错误;
而两个正方形,对应角都是90°,对应边的比也都相当,故一定相似,C正确.
故选C.
考点:相似多边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7 ,它的实际长度约为( )
,它的实际长度约为( )
A.0.266 ; ; | B.2.66 ; ; | C.26.6 ; ; | D.266 . . |
如图,在△ 中,点
中,点 分别在
分别在 边上,
边上, ∥
∥ ,若
,若 ,
, ,则
,则 等于
等于
A. | B. | C. | D. |
如图,在△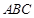 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
,  ,
, 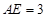 ,则
,则 的长为( )
的长为( )
| A.3 | B.6 | C.9 | D.12 |
设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d.
(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下
表:(6分)
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a-r<d<a+r | |
| d=a-r | |
| d<a-r | |
当r<a时,⊙O与正方形的公共点的个数可能有 个;
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:(5分)
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | |
| d=a+r | |
| a≤d<a+r | |
| d<a | |

所以,当r=a时,⊙O与正方形的公共点个数可能有 个;
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=
 a;(5分)
a;(5分)
如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
| A.(2,4) | B.(-1,-2) |
| C.(-2,-4) | D.(-2,-1) |
 中,
中, ,
, ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
, ,垂足为
,垂足为 .若
.若 ,则△
,则△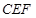 的面积是( )
的面积是( )