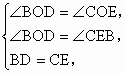Question

请先阅读下面的题目与证明，然后回答问题：

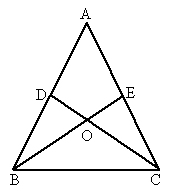
如图所示，在△ABC中，∠ABC=∠ACB，D、E分别是AB、AC上两点，且BD=CE，BE、CD相交于点O．求证：△BOD≌△COE．

证明：在△DBC和△ECB中，

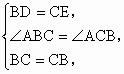
∴△DBC≌△ECB(SAS)．

∴∠DBC－∠BOC=∠ECB－∠BOC．

即△BOD≌△COE

上述证明是否有错误，若正确，请在右边空白处写上“正确”二字；如有错误，请指出从哪一步开始出现错误，并从这步开始，在下边空边处写上正确的证明过程．

Answer 1

答案：
解析：

有错误，错在“∴∠DBC－∠BOC=∠ECB－BOC”这一步，应改为： ∴∠BDC=∠CEB． 在△BOD和△COE中， ∴△BOD≌△COE(AAS)．

提示：

对于两个图形之间不能应用等式性质，等式性质仅适用于两个数量之间的关系．