题目内容
汽车在沿坡比为1：
的斜坡上前进150米，则汽车上升的高度为
- A.75米
- B.
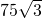米 - C.
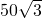
- D.150米
A
分析：首先根据题意作图，然后由汽车在沿坡比为1：，即可求得∠B的度数，继而根据在直角三角形中，30°角所对的直角边等于斜边的一半，即可求得汽车上升的高度．
解答：
解：如图：AE⊥BC于E，
由题意得：AE：BE=1：，AB=150米，
∵tan∠B=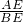
=
=
，
∴∠B=30°，
∴在Rt△ABE中，AE=
AB=×150=75（米）．
故选A．
点评：此题考查了坡角坡度问题．此题难度不大，解题的关键是根据题意作出图形，利用数形结合的思想求得坡角的度数，继而利用直角三角的性质即可求得答案．
分析：首先根据题意作图，然后由汽车在沿坡比为1：
，即可求得∠B的度数，继而根据在直角三角形中，30°角所对的直角边等于斜边的一半，即可求得汽车上升的高度．解答：
解：如图：AE⊥BC于E，由题意得：AE：BE=1：
，AB=150米，∵tan∠B=
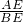==，∴∠B=30°，
∴在Rt△ABE中，AE=
AB=×150=75（米）．故选A．
点评：此题考查了坡角坡度问题．此题难度不大，解题的关键是根据题意作出图形，利用数形结合的思想求得坡角的度数，继而利用直角三角的性质即可求得答案．
练习册系列答案
相关题目
