题目内容
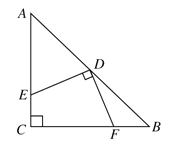
【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
【答案】证明见解析.
【解析】
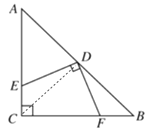
试题分析:首先可判断△ABC是等腰直角三角形,连接CD,根据全等三角形的判定易得到△ADE≌△CDF,继而可得出结论.
试题解析:如图,连接CD.∵BC=AC,∠BCA=90°,∴△ABC是等腰直角三角形,∵D为AB中点,∴BD=CD=AD,CD平分∠BCA,CD⊥AB.∵∠A+∠ACD=∠ACD+∠FCD=90°,∴∠A=∠FCD,∵∠CDF+∠CDE=90°,∠CDE+∠ADE=90°,∴∠ADE=∠CDF,在△ADE和△CFD中,∵∠A=∠FCD,AD=CD,∠ADE=∠CDF,∴△ADE≌△CFD(ASA),∴DE=DF.

练习册系列答案
相关题目
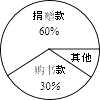
【题目】为了了解市民对“汕头市创建全国文明城市”的态度,某一天,小明等同学在本市的甲、乙和丙三个村的村民进行了一次随机调査,结果如图表:
村民态度 | 甲村 | 乙村 | 丙村 | 合计 |
关注 | 20 | 75 | 55 | 150 |
一般 | 23 | 5 | 17 | 45 |
不关心 | 57 | 20 | 28 | 105 |

(1)请将频数分布直方图补充完整;
(2)此次共调查了多少人?并求出一般在扇形统计图中所占圆心角的度数.
(3)用您学过的统计知识来说明哪个村的调査结果更能反映市民对“创文”的态度,请写出一句“创文”的宣传语.