Question

【题目】如图，在矩形ABCD中，AB=4，BC=6，若点P在AD边上，连接BP、PC，△BPC是以PB为腰的等腰三角形，则PB的长为 ．

Answer 1

【答案】5或6
【解析】解：如图，

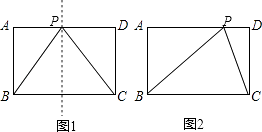
在矩形ABCD中，AB=CD=4，BC=AD=6．

如图1，当PB=PC时，点P是BC的中垂线与AD的交点，则AP=DP= AD=3．

在Rt△ABP中，由勾股定理得 PB= = =5；

如图2，当BP=BC=6时，△BPC也是以PB为腰的等腰三角形．

综上所述，PB的长度是5或6．

所以答案是：5或6．

【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念，掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．