题目内容
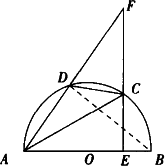
 如图,AB是⊙O的直径,CD⊥AB于D,AD=9cm,DB=4cm,求CD和AC的长.
如图,AB是⊙O的直径,CD⊥AB于D,AD=9cm,DB=4cm,求CD和AC的长.
 解:连接BC,因AB是⊙O的直径,CD⊥AB于D,所以构成双垂直三角形,
解:连接BC,因AB是⊙O的直径,CD⊥AB于D,所以构成双垂直三角形,由△ADC∽△CDB得
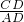 =
= ,
,即CD2=AD•DB=36,求得CD=6cm,
由△ADC∽△ACB,得
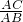 =
=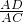 ,
,即AC2=AB•AD=117,
解得AC=3
 cm.
cm.答:CD的长为6cm;AC的长为3
 cm.
cm.分析:连接BC,构成双垂直三角形,由△ADC∽△ACB,△ADC∽△CDB得比例式,即可解题.
点评:此题主要考查学生对相似三角形的判定与性质和圆周角定理的理解与掌握,难度不大,关键是作好辅助线.此题也可不用相似三角形的判定与性质,可利用圆周角定理,射影定理和勾股定理解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )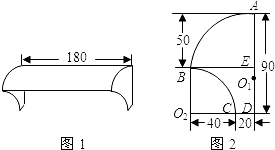 0.1平方米)
0.1平方米)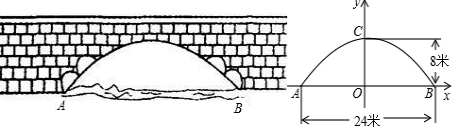
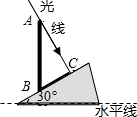 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为