题目内容
小明与小亮玩游戏，他们将牌面数字分别是2，3，4的三张扑克牌充分洗匀后，背面朝上放在桌面上．规定游戏规则如下：先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再从中随机抽出一张牌，将牌面数字作为个位上的数字．如果组成的两位数恰好是2的倍数．则小明胜；如果组成的两位数恰好是3的倍数．则小亮胜．你认为这个游戏规则对双方公平吗？请用画数状图或列表的方法说明理由．
分析：游戏是否公平，关键要看是否游戏双方赢的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
解答：解：这个游戏规则对双方不公平．
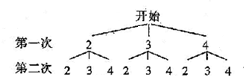
理由如下．根据题意．画树状图为：
评分说明：如果考生在表中直接写成两位教，只要正确也可得（4分）．
由树状图（或表格）可以看出，所有可能出现的结果共有9种，
分别是：22，23，24，32，33，34，42，43，44，
而且每种结果出现的可能性都相同，
而其中组成的两位数是2的倍数的结果共有6种，是3的倍数的结果共有3种．
∴P（小明胜）=
=
，
∴P（小亮胜）=
=
∴P（小明胜）＞P（小亮胜），∴这个游戏规则对双方不公平．
理由如下．根据题意．画树状图为：
| 第一次 第二次 | 2 | 3 | 4 |
| 2 | （2，2） | （2，3） | （2，4） |
| 3 | （3，2） | （3，3） | （3，4） |
| 4 | （4，2） | （4，3） | （4，4） |
由树状图（或表格）可以看出，所有可能出现的结果共有9种，
分别是：22，23，24，32，33，34，42，43，44，
而且每种结果出现的可能性都相同，
而其中组成的两位数是2的倍数的结果共有6种，是3的倍数的结果共有3种．
∴P（小明胜）=
| 6 |
| 9 |
| 2 |
| 3 |
∴P（小亮胜）=
| 3 |
| 9 |
| 1 |
| 3 |
∴P（小明胜）＞P（小亮胜），∴这个游戏规则对双方不公平．
点评：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
