题目内容
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
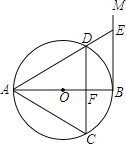
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)由AB是⊙O的直径,BM是⊙O的切线,得到AB⊥BE,由于CD∥BE,得到CD⊥AB,根据垂径定理得到![]() =
=![]() ,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证得;
,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证得;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=![]() AE,ON=
AE,ON=![]() AO,设⊙O的半径为:r则ON=
AO,设⊙O的半径为:r则ON=![]() r,AN=DN=
r,AN=DN=![]() r,由于得到EN=2+
r,由于得到EN=2+![]() r,BE=AE=
r,BE=AE=![]() ,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
(1)证明:∵AB是⊙O的直径,BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BE,
∴AB⊥CD,
∴![]() =
=![]() ,
,
∴AD=AC,
∵DA=DC,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=![]() AE,ON=
AE,ON=![]() AO,
AO,
设⊙O的半径为:r,
∴ON=![]() r,AN=DN=
r,AN=DN=![]() r,
r,
∴EN=2+![]() r,BE=
r,BE=![]() AE=
AE=![]() ,
,
在Rt△NEO与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即(![]() )2+(2+
)2+(2+![]() )2=r2+(
)2=r2+(![]() )2,
)2,
∴r=2![]() ,
,
∴OE2=(![]() )2+25=28,
)2+25=28,
∴OE=2![]() .
.


练习册系列答案
相关题目