Question

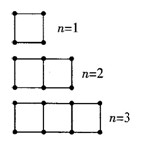如图，由火柴棒拼出的一列图形中，第n个图形由n个正方形组成，请问：
（1）第4个图形中火柴棒有几根？
（2）第n个图形中火柴棒有几根？
（3）已知最后一个图形由691根火柴棒组成，那么这个图形是由几个正方形组成？

Answer 1

解：（1）第4个图形中有四个正方形，水平放置的上边一排有4根，下边一排有4根，竖直放置的有5根，因而共有13根火柴棒．

（2）第n个图形，一排中有n各正方形，上边横放的火柴棒有n根，同理，下面横放的火柴棒也有n根，竖直放置的有n+1根，因而第n个图形中火柴棒有3n+1根．

（3）设有n个正方形组成，则得到：3n+1=691，
解得：n=230．
即这个图形是由230个正方形组成．
分析：一排中有n个正方形时，上边横放的火柴棒有n根，同理，下面横放的火柴棒也有n根，竖直放置的有n+1根，因而第n个图形中火柴棒有3n+1根．第三问中：由691根火柴棒，根据第n个图形中火柴棒有3n+1根，可列出方程组，再求解．
点评：本题的关键是发现各个正方形的联系，找出其中的规律，有一定难度，要细心观察总结．