题目内容
若锐角α满足cosα< 且tanα<
且tanα< ,则α的范围是
,则α的范围是
- A.30°<α<45°
- B.45°<α<60°
- C.60°<α<90°
- D.30°<α<60°
B
分析:先由特殊角的三角函数值及余弦函数随锐角的增大而减小,得出45°<α<90°;再由特殊角的三角函数值及正切函数随锐角的增大而增大,得出0<α<60°;从而得出45°<α<60°.
解答:∵α是锐角,
∴cosα>0,
∵cosα< ,
,
∴0<cosα< ,
,
又∵cos90°=0,cos45°= ,
,
∴45°<α<90°;
∵α是锐角,
∴tanα>0,
∵tanα< ,
,
∴0<tanα< ,
,
又∵tan0°=0,tan60°= ,
,
0<α<60°;
故45°<α<60°.
故选B.
点评:本题主要考查了余弦函数、正切函数的增减性与特殊角的余弦函数、正切函数值,熟记特殊角的三角函数值和了解锐角三角函数的增减性是解题的关键.
分析:先由特殊角的三角函数值及余弦函数随锐角的增大而减小,得出45°<α<90°;再由特殊角的三角函数值及正切函数随锐角的增大而增大,得出0<α<60°;从而得出45°<α<60°.
解答:∵α是锐角,
∴cosα>0,
∵cosα<
 ,
,∴0<cosα<
 ,
,又∵cos90°=0,cos45°=
 ,
,∴45°<α<90°;
∵α是锐角,
∴tanα>0,
∵tanα<
 ,
,∴0<tanα<
 ,
,又∵tan0°=0,tan60°=
 ,
,0<α<60°;
故45°<α<60°.
故选B.
点评:本题主要考查了余弦函数、正切函数的增减性与特殊角的余弦函数、正切函数值,熟记特殊角的三角函数值和了解锐角三角函数的增减性是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若锐角α满足cosα<
且tanα<
,则α的范围是( )
| ||
| 2 |
| 3 |
| A、30°<α<45° |
| B、45°<α<60° |
| C、60°<α<90° |
| D、30°<α<60° |
 且tanα<
且tanα< ,则α的范围是( )
,则α的范围是( ) 且tanα<
且tanα<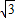 ,则α的范围是( )
,则α的范围是( ) 且tanα<
且tanα< ,则α的范围是( )
,则α的范围是( ) 且tanα<
且tanα<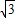 ,则α的范围是( )
,则α的范围是( )