题目内容
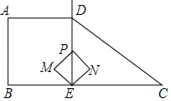
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,射线ED⊥BC于点E,AD=AB=BE=![]() BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
(1)当点N落在边DC上时,求t的值.
(2)求S与t的函数关系式.
(3)当正方形PMEN被直线BD分成2:1两部分时,直接写出t的值.
【答案】(1)t=2s时,点N落在边DC上;(2)S=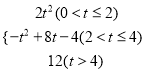
(3)t=3s或6s时,正方形PMEN被直线BD分成2:1两部分
【解析】试题分析: ![]() 当点N落在边DC上时,点P与D重合,
当点N落在边DC上时,点P与D重合, ![]() 即可求出
即可求出![]() 的值.
的值.
![]() 分
分![]() ,
, ![]() 和
和![]() 三种情况进行讨论.
三种情况进行讨论.
![]() 分两种情况进行讨论.
分两种情况进行讨论.
试题解析:(1)如图1中,当点N落在边DC上时,
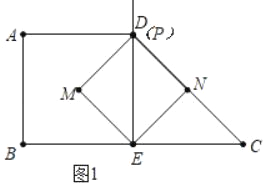
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴当点P与D重合时,点N落在CD上,
∵![]()
∴![]() 时,点N落在边DC上;
时,点N落在边DC上;
(2)①如图2中,当![]() 时,重叠部分是正方形EMPN,
时,重叠部分是正方形EMPN, ![]()
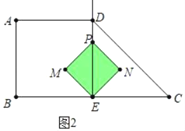
②如图3中,当![]() 时,重叠部分是五边形EFDGM,
时,重叠部分是五边形EFDGM,
![]()
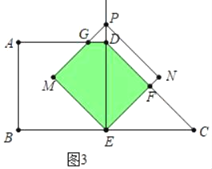
③如图4中,当![]() 时,重叠部分是四边形EFDA,
时,重叠部分是四边形EFDA, ![]()
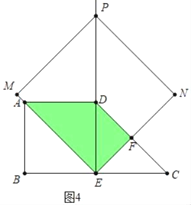
综上所述, 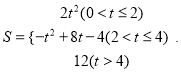
(3)①如图5中,设EM交BD于G,当![]() 时,
时,
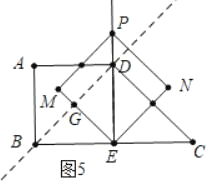
![]()
∴![]()
∴![]()
∴![]()
∴![]()
②如图6中,当![]() 时,
时, ![]()
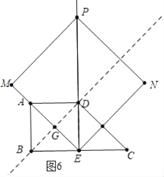
综上所述,t=3s或6s时,正方形PMEN被直线BD分成2:1两部分;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目