题目内容
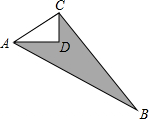 如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.求图中阴影部分的面积.
如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.求图中阴影部分的面积.分析:先根据勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACB为直角三角形,再根据S阴影=
AC×BC-
AD×CD即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:在Rt△ADC中,
∵CD=6米,AD=8米,BC=24米,AB=26米,
∴AC2=AD2+CD2=82+62=100,
∴AC=10米,(取正值).
在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676.
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°.
∴S阴影=
AC×BC-
AD×CD=
×10×24-
×8×6=96(米2).
答:图中阴影部分的面积为:96米2.
∵CD=6米,AD=8米,BC=24米,AB=26米,
∴AC2=AD2+CD2=82+62=100,
∴AC=10米,(取正值).
在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676.
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°.
∴S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:图中阴影部分的面积为:96米2.
点评:本题考查的是勾股定理的运用和勾股定理的逆定理运用,解题的关键是根据勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACB为直角三角形.

练习册系列答案
相关题目
 在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼睛距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )
在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼睛距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( ) (2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )
(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( ) 如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.图中阴影部分的面积=________.
如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.图中阴影部分的面积=________.