题目内容
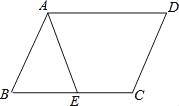
【题目】在平行四边形ABCD中,E为BC边上的一点.连结AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF:FA的值.
【答案】(1)证明见解析;
(2)EF:FA=1:2.
【解析】
试题分析:(1)根据平行四边形的对边互相平行可得AD∥BC,再根据两直线平行,内错角相等可得∠AEB=∠EAD,根据等边对等角可得∠ABE=∠AEB,即可得证;
(2)由四边形ABCD是平行四边形,可证得△BEF∽△AFD,即可求得EF:FA的值.
试题解析:(1)在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD,
∵AE=AB,
∴∠ABE=∠AEB,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠DAE=∠D;
(2)∵四边形ABCD是平行四边形,
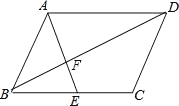
∴AD∥BC,AD=BC,∴△BEF∽△AFD,∴![]() =
=![]() ,∵E为BC的中点,∴BE=
,∵E为BC的中点,∴BE=![]() BC=
BC=![]() AD,
AD,
∴EF:FA=1:2.

练习册系列答案
相关题目
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为( )
A.140 B.138 C.148 D.160