题目内容
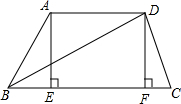已知如图梯形ABCD中，AD∥BC，∠ABC=60°，BD=2| 3 |
分析：利用已知条件先求出高，再利用直角三角形求出BF长，即可求出EF的长，而AD=EF，所以EF的长就是AD的长．
解答：解：∵∠ABC=60°，
∴∠BAD=120°，∠BAE=30°，
∴AB=2，AE=
，
在△BDF中BF=
=3，
∴EF=3-1=2，
∵AD=EF，
∴AD=2．
∴∠BAD=120°，∠BAE=30°，
∴AB=2，AE=
| 3 |
在△BDF中BF=
| 12-3 |
∴EF=3-1=2，
∵AD=EF，
∴AD=2．
点评：本题的关键是利用解直角三角形来求EF的长，即是AD的长，难度一般．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
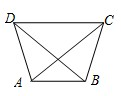已知如图所示，梯形ABCD中AB∥CD，AD=BC，AC⊥BD，AB=3，CD=5，则梯形的面积是
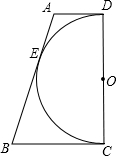如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD，下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形与半圆的面积之比（ ）
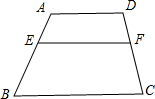如图，已知：在梯形ABCD中，AD∥BC，AD=3，BC=5，点E在AB上，且AE：EB=2：3，过点E作EF∥BC交CD于F，求EF的长？
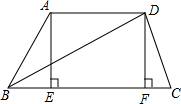已知如图梯形ABCD中，AD∥BC，∠ABC=60°，BD=2
，AE、DF为梯形的高，且BE=1，求AD的长．