题目内容
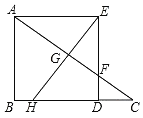
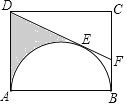
【题目】矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=![]() ,则阴影部分的面积为_____.
,则阴影部分的面积为_____.
【答案】9![]() ﹣3π
﹣3π
【解析】
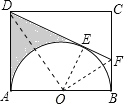
连接OF、OE、OD,如图,在Rt△OBF中利用三角函数的定义求出∠OFB=60°,再利用切线的性质和切线长定理得到∠OFE=∠OFB=60°,OE⊥DF,所以∠BFE=120°,则∠ADE=60°,同样可得∠ADO=∠EDO=30°,利用含30度的直角三角形三边的关系求出AD=![]() OA=3
OA=3![]() ,所以S△ADO=
,所以S△ADO=![]() ;接着计算出∠AOE=120°,于是得到S扇形AO=3π,然后利用阴影部分的面积=四边形AOED的面积-扇形AOE的面积进行计算即可.
;接着计算出∠AOE=120°,于是得到S扇形AO=3π,然后利用阴影部分的面积=四边形AOED的面积-扇形AOE的面积进行计算即可.
解:连接OF、OE、OD,如图,
在Rt△OBF中,∵tan∠OFB=![]() =
=![]() =
=![]() ,
,
∴∠OFB=60°,
∵BF⊥AB,
∴BF为切线,
∵DF为切线,
∴∠OFE=∠OFB=60°,OE⊥DF,
∴∠BFE=120°,
∵BC∥AD,
∴∠ADE=60°,
∵AD⊥AB,
∴AD为切线,
而DE为切线,
∴∠ADO=∠EDO=30°,
在Rt△AOD中,AD=![]() OA=3
OA=3![]() ,
,
∴S△ADO=![]() ×3×3
×3×3![]() =
=![]() ;
;
∵∠AOE=180°﹣∠ADE=120°,
∴S扇形AOE=![]() =3π,
=3π,
∴阴影部分的面积=四边形AOED的面积﹣扇形AOE的面积=2×![]() ﹣3π=9
﹣3π=9![]() ﹣3π.
﹣3π.
故答案为9![]() ﹣3π.
﹣3π.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目