题目内容
(2005•青岛)小明的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小明想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离,于是小明在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°,已知公寓楼AD的高为60米,请你帮助小明计算出大厦的高度BC.
【答案】分析:在图中有两个直角三角形,即RT△DEB和RT△ABC,若设DE=x,则根据30°、60°角的正切值可求得BC和BE,然后根据二者之间的关系,得到一个关于x的方程解答即可.
解答: 解:如图,由题意知:四边形ACED是矩形.
解:如图,由题意知:四边形ACED是矩形.
∴AC=DE,DA=EC=60米,∠BDE=30°.
设DE=x,
在Rt△BDE中,
∵tan∠BDE=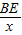 ,
,
∴BE=x×tan∠BDE=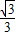 x.
x.
在Rt△BAC中,
∵tan∠BAC=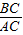 ,
,
∴BC= x,
x,
即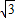 x=
x=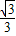 x+60,解得:x=30
x+60,解得:x=30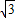 ,
,
∴BC=BE+EC=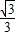 x+60=
x+60=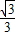 ×30
×30 +60=90(米).
+60=90(米).
答:大厦的高度BC为90米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
解答:
 解:如图,由题意知:四边形ACED是矩形.
解:如图,由题意知:四边形ACED是矩形.∴AC=DE,DA=EC=60米,∠BDE=30°.
设DE=x,
在Rt△BDE中,
∵tan∠BDE=
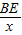 ,
,∴BE=x×tan∠BDE=
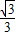 x.
x.在Rt△BAC中,
∵tan∠BAC=
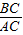 ,
,∴BC=
 x,
x,即
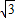 x=
x=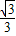 x+60,解得:x=30
x+60,解得:x=30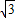 ,
,∴BC=BE+EC=
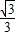 x+60=
x+60=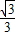 ×30
×30 +60=90(米).
+60=90(米).答:大厦的高度BC为90米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目