题目内容
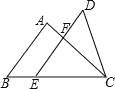
【题目】(2016浙江省舟山市第15题)如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE∥AB交AC于点F，AB=12，EF=9，则DF的长是多少？
【答案】7
【解析】
试题分析：根据题意，易得△CDF与四边形AFEB的面积相等，再根据相似三角形的相似比求得它们的面积关系比，从而求DF的长，∵△ABC与△DEC的面积相等，∴△CDF与四边形AFEB的面积相等，
∵AB∥DE，∴△CEF∽△CBA，∵EF=9，AB=12，∴EF：AB=9：12=3：4，
∴△CEF和△CBA的面积比=9：16，设△CEF的面积为9k，则四边形AFEB的面积=7k，
∵△CDF与四边形AFEB的面积相等，∴S△CDF=7k，∵△CDF与△CEF是同高不同底的三角形，
∴面积比等于底之比，∴DF：EF=7k：9k，∴DF=7．
练习册系列答案
阅读快车系列答案
相关题目
