题目内容
【题目】(1)如图,在等边三角形ABC的边BC、AC上分别取点D、E,使得BD=CE,AD与BE相交于点F.求∠AFE的度数.
(2)若点D、E分别在边CB、AC的延长线上,同样BD=CE,AD与BE所在直线相交于点F.请你先画出图形,再求出∠AFE的度数.
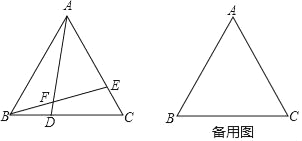
【答案】(1)∠AFE=60°;(2)画图见解析,∠AFE=60°.
【解析】整体分析:
(1)先用SAS证明△ABD≌△BCE,结合三角形的外角的性质即可求得∠AFE的度数;(2)根据题意画出图形,求AFE的度数的方法与(1)类似.
解:(1)∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中,
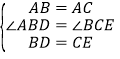
∴△ABD≌△BCE,
∴∠BAD=∠CBE.
又∵∠AFE=∠ABF+∠BAD=∠ABC
∴∠AFE=60°.
(2)如图.

∵△ABC为等边三角形,
∴AC=BC,∠ABC=∠ACB=60°.
∴∠ABD=∠BCE=120°,
∵BD=CE,
在△ABD和△BCE中,
∴△ABD≌△BCE,
∴∠DAB=∠CDE,
∵∠ABE=∠AFB+∠FAB=∠ABC+∠CBE,
∴∠AFB=∠ABC=60°,
∴∠AFE=60°.

练习册系列答案
相关题目
